NPV: что это такое и как рассчитать –

Что такое NPV и как его рассчитать: объяснение человеческим языком на простом примере

Доброго времени суток всем, кто запутался в дебрях сложных терминов и запутанных формулировок. Гуру от экономики рассуждают о доходности инвестиционных проектов, но понять их все труднее. Вместо слов сплошная абракадабра. Например, показатель NPV: что это такое и как рассчитать? И главное — зачем?

Что показывает NPV

Согласитесь, спокойнее за свои деньги, если в вопросах инвестирования полагаешься не только на интуицию или советы неизвестно насколько умных дяденек.

Net Present Value — так на английском языке расшифровывается аббревиатура. Переводится словосочетание по-разному, чаще всего используется название ЧПС (чистая приведенная стоимость), реже — чистый дисконтированный доход (ЧДС) или чистая текущая стоимость (ЧТС).

Понятнее не стало, правда? Я буду использовать английское название NPV, а разбираться с ним по-русски и на примерах.

NPV показывает, насколько выгодно вкладывать средства в тот или иной инвестиционный проект. Казалось бы, все просто: вложил тысячу, получил через пять лет полторы — выгодно. 50 % чистой прибыли! На самом деле полученные деньги к этому времени могут стоить дешевле вложенных.

Рассчитывают NPV, если требуется:

• оценить доходность инвестиций и сроки, когда можно ожидать прибыль
• сравнить несколько предложений и выбрать наиболее удачное.

Экономический смысл показателя простыми словами

NPV – это результат сложения всех доходов и расходов (входящих и исходящих денежных потоков) с учетом изменения ценности денег со временем (дисконтирования).

Прогноз результатов инвестиций (вложения денег) в зависимости от полученного значения NPV.

0	Есть вероятность вернуть вложенные средства в полном объеме или с минимальной прибылью
>0	Прибыльное вложение
	Убыточный проект

Сложности расчетов

По формуле рассчитать NPV нетрудно, достаточно навыков, полученных на уроках математики.

Задачка для шестиклассника. Вася Петров дал Пете Курочкину 100 рублей год назад и 20 рублей вчера. Сколько денег получит Вася через три года, если Петя обещал вернуть на 24 % больше полученной суммы?

Рассчитанный результат должен учитывать реальную стоимость денег на текущий момент, а она зависит не только от инфляции. Верный NPV, то есть тот, что даст нам самую точную оценку, зависит от правильности определения величины ставки дисконтирования. Вот в чем сложность!

А Васю Петрова на самом деле интересует, хватит ли ему на велосипед, который год назад стоил 117 рублей, а сейчас 126.

Денежные потоки и куда они текут

Денежными потоками называют движение финансов. Запомнить просто:

• отдаем деньги — отрицательный поток
• получаем — положительный.

Ставка дисконтирования

Эта процентная ставка используется, чтобы рассчитать стоимость денег в будущем. Величина ее зависит от множества показателей и определяется на год, месяц или квартал – смотря какие факторы учитываются и на какие периоды времени разбивается проект.

Все, что надо для расчета

Данные, чтобы рассчитать NPV:

• i — ставка дисконтирования конкретного проекта;
• N — количество периодов;
• CF — сумма чистого денежного потока (доходы минус расходы);
• t — период времени, за который считаем чистый денежный поток.

Два способа посчитать NPV в Excel

Я назову героем того, кто рассчитает такую формулу на листочке. Excel в помощь обычным людям:

1. Создать таблицу, в ее верхней части занести по периодам суммы инвестиций, расходов и доходов по проекту.
2. Рассчитать чистый денежный поток.

Дальше выбрать один из способов расчета:

1. Занести i для проекта по периодам. Разбить формулу на блоки и последовательно рассчитать до конечного результата. На примере показана следующая последовательность: начала знаменатель, затем дисконтированный денежный поток за период. Суммировать полученные результаты.

Этот способ имеет свои преимущества, он больше подходит, если:

• нужно видеть промежуточные результаты;
• ставка дисконтирования в различные периоды отличается.

1. Использовать встроенную формулу Excel. Выбрать в блоке финансовых формул – она называется ЧПС. Заполнить поля: ставка дисконтирования и диапазон суммирования (значения чистого денежного потока по периодам).

Ниже я покажу, что результаты при единой ставке дисконтирования на все периоды совпадают.

Расчет NPV: за и против

Перед тем как приступить к проверке, следует понять, что NPV не единственный и идеальный способ оценки доходности инвестиционного проекта. Достоинства показателя в применении ставки дисконтирования, которая позволяет учесть:

• изменение стоимости денег со временем;
• риски по проекту.

Но есть и недостатки:

1. Есть вероятность неточного определения ставки, если не учтен хотя бы один фактор риска.
2. Ни один прогноз не дает стопроцентной гарантии совпадения ожидаемого результата с действительным.

Пример расчета

Тем, кто не опустил руки при чтении предыдущего раздела, демонстрирую работоспособность таблицы с расчетами.

Возьму любые цифры, похожие на инвестиционный проект: первоначальные вложения инвестиция, увеличивающиеся суммы выплат и суммы текущих расходов по проекту. Ставку дисконтирования определю в 10 %.

Примеры расчета в бизнес-планах

NPV полезно использовать при составлении бизнес-планов. Пример (цифры я взял с потолка, список статей расходов и доходов оттуда же).

Задумал я открыть модное заведение барбершоп (парикмахерская для бородачей, если кто не в курсе). Рассчитаю, когда заведение начнет приносить доход.

• 6 рабочих мест
• 12 рабочих часов
• средний чек 3000
• среднее время обслуживания одного клиента 1,5 часа
• средняя загрузка 50 %.

Сразу мне надо потратить 15 000 000:

• оформление документов
• первый взнос на аренду помещения
• ремонт
• оборудование и оснащение рабочих мест
• реклама
• вывески
• сайт с онлайн-записью.

Месяц на обустройство, и потекли денежки в разные стороны.

Доходы – выручка от продажи услуг. При полной загрузке это 4 320 000 в месяц. 50 % – 2 160 000.

• зарплата персонала 1 080 000
• расходные материалы 432 000
• аренда 150 000
• реклама 30 000.

Определяем дисконт 10 %, ну ладно, 15 %.

В первый год доходы поступают только 11 месяцев, то есть 23 760 000. Далее по 12 месяцев. 25 920 000 в год. Расходы, к сожалению, тоже постоянные. Суммирую и умножаю на 11 в первый год, далее на 12, итого 18 612 000 и 20 304 000 соответственно.

Барабанная дробь! Дорогая, собирайся, через пять лет мы едем в отпуск!

Подводим итоги

Ну, вот и все. Теперь некоторые непонятные слова стали простыми и даже привычными. Выяснилось, что деньги сегодня и через несколько лет – это разные деньги, а выбирать из разнообразных предложений более выгодное нужно не потому, что приятель расхваливает, а потому, что у него NPV выше остальных. Не у приятеля, конечно.

И бонусная «пятерочка в карму»: этими ценными знаниями можно осчастливить любого желающего. Например, друзей в соцсетях. Мне не жалко, я еще напишу — подписывайтесь и читайте на здоровье. Удачных инвестиций!

NPV (Net Present Value) и оценка эффективности проектов

Если говорить просто и понятно, это показатель того, какую прибыль получит инвестор от проекта. Примечательно, что NPV показывает финансовый результат в эквиваленте сегодняшней суммы. Это особенно важно, поскольку сегодняшняя тысяча долларов не будет равна 1000 долларов через 5 или 10 лет.

Благодаря этому показателю вы можете сравнить предполагаемые результаты в разные инвестиции и выбрать наиболее привлекательный вариант.

Пример расчёта NPV

Пример расчета для трёх условных проектов позволяет, как рассчитать NPV, так и определить, какой из проектов будет более привлекательным для инвестирования.

Согласно условиям примера:

• начальные инвестиции – ICo – в каждый из трёх проектов равны 400 у.е.,
• норма прибыли – ставка дисконтирования – составляет 13%,
• прибыль, которые могут приносить проекты (по годам), расписана в таблице на 5-летний срок.

Рассчитаем чистый дисконтированный доход, чтобы выбрать наиболее выгодный для инвестирования проект. Фактор дисконтирования 1/(1 + R)t для интервала в один год будет t = 1: 1/(1+0,13)1 = 0,885. Если пересчитать NPV каждого сценария по годам с подстановкой в формулу определяющих значений, то получается, что для первого проекта NPV= 0,39, для второго – 10,41, для третьего – 7,18.

По этой формуле чистый приведённый доход выше всего у второго проекта, поэтому, если основываться только на параметре NPV, то он и будет самым привлекательным для инвестиций с точки зрения прибыли.

Однако сравниваемые проекты могут иметь разную продолжительность (жизненный цикл). Поэтому нередки ситуации, когда, например, при сравнении трёхлетнего и пятилетнего проектов NPV будет больше у пятилетнего, а среднее значение по годам – у трёхлетнего. Чтобы не возникло противоречий, рассчитываться в таких ситуациях должна ещё и среднегодовая норам доходности (IRR).

Кроме того, объём первоначальных инвестиций и ожидаемая прибыль известны не всегда, что создаёт сложности в применении расчётов.

Возможные сложности при расчете

При расчете ориентируются на несколько оценок и предположений, так как показатель может содержать ошибки. После первого анализа необходим повторный, чтобы перепроверить оценки.

Результаты расчета могут стать ошибочными, если не учитывать следующие факторы:

1. Ставка дисконтирования. Сегодня вы используете процент на конкретный момент времени, чтобы рассчитать доходы. Однако через несколько лет процентная ставка значительно вырастет, а стоимость средств, вложенных в проект, увеличится. Иными словами, доходы, которые вы планировали, за конкретный год окажутся менее ценными.
2. Первоначальные инвестиции. Если вы закупаете оборудование по фиксированной цене, проблем не возникнет. Если же вам постоянно требуется обновлять оборудование в процессе производства, рассчитанная сумма станет весьма условной.

Два способа посчитать NPV в Excel

Я назову героем того, кто рассчитает такую формулу на листочке. Excel в помощь обычным людям:

1. Создать таблицу, в ее верхней части занести по периодам суммы инвестиций, расходов и доходов по проекту.
2. Рассчитать чистый денежный поток.

Дальше выбрать один из способов расчета:

1. Занести i для проекта по периодам. Разбить формулу на блоки и последовательно рассчитать до конечного результата. На примере показана следующая последовательность: начала знаменатель, затем дисконтированный денежный поток за период. Суммировать полученные результаты.

Этот способ имеет свои преимущества, он больше подходит, если:

• нужно видеть промежуточные результаты;
• ставка дисконтирования в различные периоды отличается.

1. Использовать встроенную формулу Excel. Выбрать в блоке финансовых формул – она называется ЧПС. Заполнить поля: ставка дисконтирования и диапазон суммирования (значения чистого денежного потока по периодам).

Ниже я покажу, что результаты при единой ставке дисконтирования на все периоды совпадают.

Ставки дисконтирования

Ставка дисконтирования – это процентная ставка. Она используется, чтобы переоценить стоимость будущего капитала на текущий момент. Иными словами, любая сумма, которая у вас сейчас на руках, оценивается больше, чем в дальнейшем. 10 000 рублей сегодня – это ценнее, чем 10 000 рублей через 5 лет.

Вложив сейчас 10 000 рублей, неважно, в банк или в проект, в будущем вы получите, допустим, 15 000 рублей. Разница между этими двумя силами, выраженная в процентах, и есть процентная ставка.

Преимущества и недостатки

Достоинства метода заключаются в следующем:

1. NPV учитывает временной фактор – изменение стоимости денег и длительность жизненного цикла инвестиционного проекта.
2. В немалой степени отражает основные критерии эффективности инвестиций: оценка рисков, расчет срока окупаемости и разницы между доходами и расходами с учетом инфляции.

1. Спрогнозировать денежные потоки непросто – всегда найдутся факторы, которые невозможно принять во внимание заранее.
2. Сложный механизм расчета ставки дисконтирования. Точнее, сложность не в формуле ее расчета, а в выборе правильного метода. Выбрав неподходящий метод, можно получить значение NPV, далекое от истины.

Пример расчета

Для примера расчета возьму две фирмы – А и Б.

Фирмы	А	Б
Вложения	— 1 000 000	— 500 000
Поступление денег в первый год (F1)	800 000	200 000
Поступление денег во второй год (F2)	500 000	510 000
Приведенная стоимость F1 и F2 при ставке дисконтирования 10%. Показывает, сколько вы должны вложить сегодня, чтобы получить значение F1 и F2. Р=Fn/(1+r)^n, где Fn – будущая стоимость, r – средняя ставка дисконтирования, n – временной промежуток	1 140 496	603 306
NPV (приведенная стоимость – вложения)	140 496	103 306

NPV у фирмы А выше. В обоих случаях показатель положителен, значит, проект принимается.

Формула NPV

Рассчитывают чистый дисконтированный доход по формуле расчета, которая в упрощённом виде выглядит как PV – ICo, где PV представляет собой текущие показатели денежного потока, а ICo – размер первоначальной инвестиции. В более сложном виде, где показан механизм дисконтирования, формула выглядит следующим образом:

NPV= — ICo + ∑nt=1 CFt / (1 + R)t

Здесь:

• NPV – чистый дисконтированный доход.
• CF – Cash Flow – денежный поток (инвестиционные платежи), а t рядом с показателем – время, в течение которого осуществляется денежный поток (например, годичный интервал).
• R – Rate – дисконт (ставка: коэффициент, который дисконтирует потоки).
• n – количество этапов реализации проекта, определяющее длительность его жизненного цикла (например, количество лет).
• ICo – Invested Capital – начальный инвестируемый капитал.

Таким образом, NPV рассчитывается как разность совокупных денежных потоков, актуализированных на определённый момент времени по факторам риска и первоначальной инвестиции, то есть, считается инвесторская прибыль как добавочная стоимость проекта.

Поскольку для инвестора важно не только выгодное вложение, но и грамотное управление капиталом на протяжении продолжительного времени, данная формула может быть ещё расширена так, чтобы предусматривать не разовые, а дополнительные периодические вложения и коэффициент инфляции (i)

NPV= ∑nt=1 CFt / (1 + R)t — ∑mj =1 ICj / (1 + i)j

Примеры расчета в бизнес-планах

Приведу следующие данные: первоначальные вложения -150 млн руб., поступление в первый год – 30 млн руб., во второй и третий по 70 млн руб., в четвертый – 45 млн руб. Далее я рассмотрю два случая – стоимость капитала неизменна в 12 %, и она будет меняться по годам – 12, 13, 14, 14%.

Первый случай: по формуле

получаем, что NPV = 11,0 млн руб, значит, проект принимается.

Во втором случае я получаю следующий результат:

Это говорит о неприемлемости проекта.

Дисконтированные показатели оценки эффективности инвестиционного проекта

Дисконтированные показатели эффективности инвестиционных проектов включают в себя:

• чистый дисконтированный доход (ЧДД, NPV);

• дисконтированный срок окупаемости (Tок, DPР);

• индекс доходности (ДИД, DPI);

• внутренняя норма доходности (ВНД, IRR);

• чистая терминальная стоимость (NTV, ЧТС);

• модифицированная внутренняя норма прибыли (доходности) (MIRR);

• и другие.

Чистый дисконтированный доход (NPV)

Основным показателем при оценке эффективности инвестиций является чистый дисконтированный доход проекта. Именно он показывает в абсолютной величине, сколько принесет проект инвестору.

Суть чистого дисконтированного дохода заключается в следующем. NPV (ЧДД) показывает, на сколько дисконтированные притоки проекта превышают дисконтированные оттоки по нему. То есть данный показатель учитывает то, что стоимость денег меняется во времени.

Чистый дисконтированный доход (NPV) – определяется путем сопоставления величины дисконтированных инвестиций с общей суммой дисконтированных денежных поступлений, порождаемых ими в течение расчетного периода.

По своей сути NPV отражает прогнозную оценку прироста экономического потенциала предприятия в случае принятия рассматриваемого проекта.

Для расчета NPV (ЧДД) используется следующая формула:

Понятно, что, так как NPV — это доход от проекта, то он измеряется в денежных единицах.

Критерий чистого дисконтированного дохода

Для того чтобы принять решение на основе данного показателя, необходимо сравнить полученный NPV с критерием:

Если чистый дисконтированный доход равен 0, то проект окупается. Если NPV больше 0, то инвестиционную деятельность можно осуществлять.

Однако, если чистый дисконтированный доход 0, это вовсе не означает, что инвестор лишь окупит свои инвестиции. Окончательный вывод можно сделать, лишь зная принцип определения ставки дисконтирования. Ведь существуют случаи, когда нулевой чистый дисконтированный доход будет означать, что инвестор получит нормальную прибыль.

Пример расчета чистого дисконтированного дохода (NPV) при постоянной ставке дисконтирования

Рассмотрим на примере, как определить чистый дисконтированный доход проекта и по его значению принять решение об эффективности проекта.

Размер инвестиции 900 тыс. рублей. Доходы реализации бизнес-проекта составляют по годам: в первом году — 200 тыс. руб.; во втором году — 300 тыс. руб.; в третьем году — 500 тыс. руб.; в четвертом году: 500 тыс. руб. Ставка дисконтирования – 10%.

Следовательно, на основе полученных результатов примера, можно сделать вывод, что инвестор сможет окупить свои вложения и получить дополнительно 246916,19 рублей.

Пример расчета чистого дисконтированного дохода (NPV) при изменяющейся ставке дисконтирования

Необходимо обратить внимание на то, что если для каждого расчетного периода задана своя норма дисконта, то использование формулы не возможно. Это происходит из-за того, что деньги теряют свою стоимость не равномерно. Дисконтирование денежных потоков напрямую связано со ставкой дисконтирования.

Рассмотрим это на предыдущем примере. Но ставка дисконтирования в этом случае будет изменяться.

Размер инвестиции 900 тыс. рублей. Доходы реализации бизнес-проекта составляют по годам: в первом году — 200 тыс. руб.; во втором году — 300 тыс. руб.; в третьем году — 500 тыс. руб.; в четвертом году: 500 тыс. руб. Ставка дисконтирования по периодам составила: первый год – 5%, второй год — 7%, третий год — 10%, четвертый год — 15%.

Индекс доходности (DPI)

Не смотря на то, что показатель чистый дисконтированный доход, несомненно, имеет целый ряд преимуществ, но он имеет и существенный недостаток.

Этот недостаток заключается в том, что по показателю NPV (ЧДД) нельзя сравнить эффективность нескольких проектов.

Например, NPV по проекту А составил 1 млн. рублей, а по проекту В — 10 млн. рублей. Это не означает, что проект В однозначно более эффективный. Ведь инвестиционные затраты на проект Б, могут быть намного больше, чем по проекту А.

Читайте также: Методы оценки эффективности инвестиций и обоснование их экономической целесообразности по проекту

Для решения этой проблемы необходимо использование относительного показателя. Например, индекса доходности. Данный индекс может рассчитываться, как по каждому отдельному проекту (индекс доходности проекта), так и в целом по всему инвестиционному портфелю (индекс доходности проекта ).

Дисконтированный индекс доходности (DPI) – характеризует доход на единицу инвестиционных затрат и рассчитывается как отношение дисконтированных доходов по проекту к дисконтированной стоимости инвестиций.

Для определения дисконтированного индекса доходности используется следующая формула:

DPI измеряется в долях или, в связи с тем, что это экономический показатель, он может измеряться в рублях на рубль (руб./руб.).

Норма индекса доходности

На основании вышеприведенной формулы показателя можно сделать вывод, что он должен быть больше 1.

Таким образом, если полученное значение дисконтированного индекса доходности:

• больше 1, то проект приемлем;

• меньше 1, то инвестиции не оправданы.

Пример расчета индекса доходности (DPI)

Определить на основании индекса доходности, какой из 2-х проектов более эффективен, если первый требует капиталовложения в размере 100 000 рублей, а второй – 250 000 рублей. NPV первого проекта – 20 000 рублей, второго – 35 000 рублей.

Вывод: первый проект имеет больший индекс доходности, следовательно, он более привлекателен, так как более эффективен. В то же время оба проекта приемлемы.

Дисконтированный срок окупаемости (DPР)

Дисконтированный срок окупаемости (DВР) – период, по окончанию которого первоначальные инвестиции покрываются дисконтированными доходами от осуществления проекта.

Таким образом, для определения дисконтированного срока окупаемости используется слудующее неравенство.

DPP определяется также как и PP двумя способами:

• соотношением суммарного объема инвестиций со средними значениями дохода по проекту;

• сопоставления денежных притоков и оттоков по периодам. Это белее точный способ.

Критерий эффективности проекта на основе DPP

Для того чтобы инвестиционный проект был приемлем, необходимо чтобы выполнялось следующее условие:

Следовательно, дисконтированный период окупаемости должен быть больше горизонта расчета по проекту.

Внутренняя норма доходности (IRR, ВНД)

Еще одним показателем эффективности проекта является внутренняя норма доходности (IRR, ВНД). На основании расчета IRR инвестор может определить не только эффективнее проект или нет, но и какой запас прочности у него.

Внутренняя норма доходности (IRR, ВНД) – это ставка дисконтирования, при которой проект становится безубыточным, т. е. NPV = 0.

Формула для расчета внутренней нормы доходности (IRR, ВНД) имеет следующий вид:

Критерии внутренней нормы доходности проекта (IRR, ВНД)

Для принятия решения об эффективности проекта на основе внутренней нормы доходности производится ее сравнение со ставкой дисконтирования принятой по проекту:

• IRR > r => Проект приемлем;

• r = IRR => Проект окупается и приносит минимальную величину нормальной прибыли;

• IRR < r =>Проект неэффективен.

Определение внутренней нормы доходности с помощью программы Excel

Для облегчения расчетов ВНД (IRR) очень хорошо можно использовать приложение Excel. В русскоязычной версии Excel есть встроенная функция, позволяющая без труда найти значение внутренней нормы доходности.

Эта функция называется ВСД. Пример ее использование приведен на рисунке.

Как видно из рисунка, проект А имеет IRR(ВНД)=24,20%. В то время как по проекту В IRR(ВНД)=18,80%.

Это позволяет сделать следующие выводы:

• Во-первых, проект А более привлекателен, у него больше доходность, так как по нему больше значение ВНД. Следовательно, он обладает большим запасом прочности.

• Во-вторых, если ставка дисконтирования по первому проекту меньше IRR(ВНД)=24,20%, то проект в целом приемлем.

• В-третьих, если ставка дисконтирования по второму проекту меньше IRR(ВНД)=18,80%, то проект также приемлем.

Графический способ определения внутренней нормы доходности

Графический способ определения внутренней нормы доходности
∆ = (IRR — r) характеризует запас прочности проекта

Рассмотрим на предыдущем примере, в котором внутренняя норма доходности определялась с помощью программы Excel, графический способ ее нахождения.

Если например ставка дисконтирования по проекту выбрана равная 10%, то запас прочности по проекту А составит 14,2%, а по проекту В — 8,8%.

Вычисление внутренней нормы доходности методом линейной аппроксимации

Рассмотрим на примере принципы вычисления ВНД методом линейной аппроксимации. Для этого возьмем проект А, рассматриваемый ранее.

Для проекта А при ставке дисконтирования 15% NPV(ЧДД) равен 301317 рублей, а при ставке 25% NPV(ЧДД) становится отрицательным и равен -21440 рублей. Необходимо найти IRR(ВНД).

Вывод: Как мы видим значения ВНД, полученные тремя этими способами приблизительно равны. Понятно, что наиболее точный способ — это вычисление в программе Excel.

Чистая терминальная стоимость (NTV, ЧТС)

Чистая терминальная стоимость (NTV, ЧТС) – это нара­щенные чистые доходы на конец периода.

где t – анализируемый период.

Отличие чистой терминальной стоимости от чистой дисконтированной стоимости проекта заключается в том, что при расчете NPV применяется принцип дисконтирования, в то время как при расчете NTV — принцип наращивания.

Данное отличие представлено на рисунке.

Графическая интерпретация отличия NTV от NPV

Принципы принятия проекта на основе критерия NTV

Принципы оценки эффективности инвестиционного проекта на основе расчета показателя чистой терминальной стоимости (ЧТС, NTV) аналогичны принципам оценки на основе расчета чистого дисконтированного дохода (ЧДД, NPV):

• если NTV > 0, то проект следует принять;

• NTV < 0, то проект следует отвергнуть;

• в случае, когда NTV= 0, то проект не сказывается на величине ценности фирмы, а потому решение о целесообразности его принятия должно основываться на оценке дополнительных аргументов.

Пример расчета чистой терминальной стоимости проекта (ЧТС, NTV)

Требуется провести анализ инвестиционного проекта со следующими характеристиками (млн. руб.): –150, 30, 70, 70, 45.Если ставка дисконтирования ­– 12%.

млн. руб.

Вывод: Проект следует принять, т.к. NTV > 0.

Модифицированная внутренняя норма прибыли (доходности) (MIRR)

Модифицированная внутренняя норма прибыли (доходности) (MIRR) – скорректированная с учетом нормы реинвестиции внутренняя норма доходности.

Порядок расчета показателя MIRR:

Читайте также: Главным событием сегодняшнего дня станут аукционы ОФЗ 46020 и ОФЗ 46018 общим номинальным объемом 39 млрд руб, — Николай Подгузов, ИК «Ренессанс Капитал»

МСФО, Дипифр

Формула расчета NPV инвестиционного проекта. Это просто.

Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Вкладываться можно в финансовые инструменты, или в новый бизнес, или в расширение уже существующего бизнеса. В любом случае, инвестирование — это вложение денег в какие-то активы на долгосрочную перспективу.

Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?

Для этого можно воспользоваться одним из методов оценки эффективности инвестиционных проектов. NPV — это один из таких методов. Найти NPV инвестиционного проекта означает найти чистую приведенную стоимость всех денежных потоков, связанных с этим проектом.

Как это сделать, используя формулу для расчета NPV, и так ли это сложно, читайте ниже.

Что можно делать с деньгами?

Если у вас появилась некоторая сумма денег, то есть три возможности ими распорядиться:

• а) потратить — купить большую квартиру и жить в ней, купить автомобиль и ездить на нем на работу, съездить в отпуск на Гавайи. У каждого есть свои варианты, ведь, чтобы потратить деньги, советчики не нужны.
• б) спрятать в сейф на «черный день». И всё время трястись, что их украдут. И с грустью наблюдать, как они обесцениваются в результате инфляции
• в) «вложить» (инвестировать) куда-нибудь с целью получения дохода в будущем. А будет ли это выгодно?

Эта статья для тех, кто выбирает третий пункт из этого списка. И не важно, собираетесь ли вы инвестировать свои деньги или деньги компании, в которой вы будете работать финансовым специалистом.

Инвестировать можно в банк, положив деньги на депозит, а можно купить долговые обязательства или акции банков или компаний, которые свободно торгуются на финансовом рынке. Это самый простой путь, но не самый доходный. Для физических лиц, то есть нас с вами, чаще всего, это единственный способ вложения накоплений.

А можно инвестировать в бизнес, что означает купить долгосрочные активы (основные средства), используя которые в процессе производства, торговли или оказания услуг, вы будете получать в будущем притоки денежных средств. Для юридических лиц (компаний) это собственно говоря, и является целью их существования — делать деньги (прибыль) из инвестиций.

Чтобы определить, будет ли успешным тот или иной инвестиционный проект, финансовыми специалистами используются определенные методы оценки проектов. Два основных метода — это NPV и IRR.

NPV — что это такое? Какая логика в этом показателе?

NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов , основанный на методологии дисконтирования денежных потоков.

Если вы знаете перспективный бизнес-проект и хотите вложить в него деньги, то неплохо было бы для начала рассчитать NPV (=чистую приведенную стоимость) этого бизнес-проекта. Алгоритм расчета такой:

• 1) нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем
• 2) определить стоимость капитала (cost of capital) для вас — это будет ставкой дисконтирования
• 3) продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2)
• 4) Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта

Правило: если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.

Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы

• а) возместить инвестированный капитал и
• б) обеспечить необходимый доход на этот капитал.

Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем выгоднее/прибыльнее является данный проект. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.

Формула NPV — пример расчета

Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:

• n, t — количество временных периодов,
• CF — денежный поток (Cash Flow),
• R — стоимость капитала (ставка дисконтирования, Rate)

На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта А и Б, которые имеют следующую структуру денежных потоков в ближайшие 4 года:

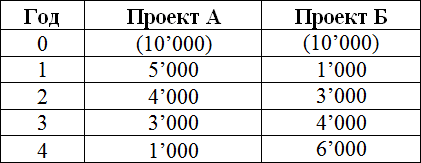
Оба проекта А и Б имеют одинаковые первоначальные инвестиции в 10,000, но денежные потоки в последующие годы сильно разнятся. Проект А предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект Б, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта А, но зато в последующие два года Проект Б принесет больше денежных средств, чем проект А.

Рассчитаем NPV инвестиционного проекта следующим образом:
Предположения для упрощения расчета:

• а) все денежные потоки случаются в конце каждого года,
• б) первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас
• б) стоимость капитала (ставка дисконтирования) составляет 10%

Про дисконтирование денежных потоков на этом сайте есть отдельная статья. Если расчет, приведенный ниже, вам покажется совсем непонятным, то лучше будет сначала вспомнить основы дисконтирования, вернувшись к этой статье.

Коротко напомню: чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».

Применим формулу NPV для Проекта А. У нас четыре годовых периода и пять денежных потоков. Первый поток (10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:

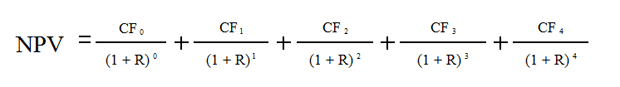
Если подставить в эту сумму данные из таблицы для Проекта А вместо CF и ставку 10% вместо R, то получим следующее выражение:

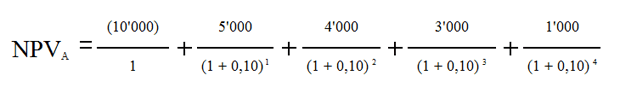
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока.

В результате приведенная стоимость денежных потоков (NPV) для проекта А равна 788,2 доллара. Расчет NPV для проекта А можно так же представить в виде таблицы и в виде шкалы времени:

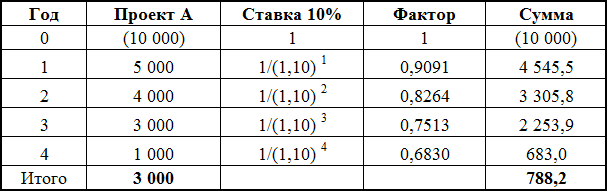
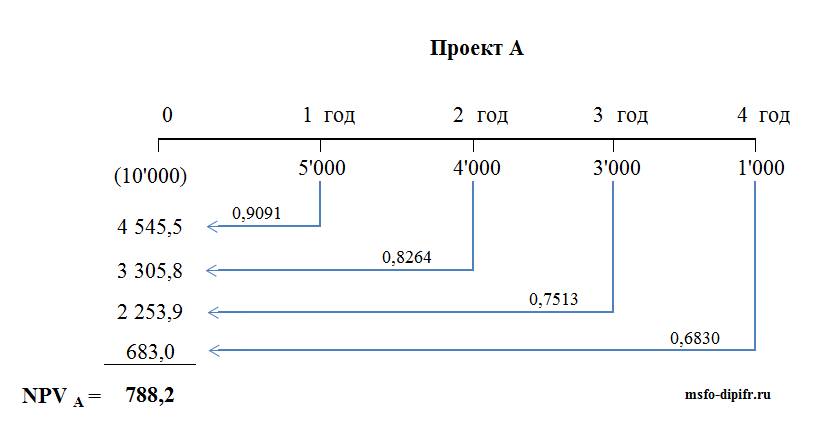
Точно таким же образом рассчитывается NPV для проекта Б.

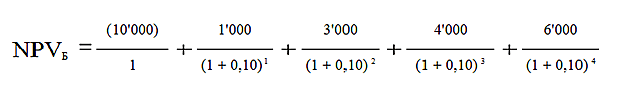
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших (4,000 и 6,000), но отдалённых по времени (третий и четвертый годы) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта Б чистая приведенная стоимость денежных потоков будет меньше, чем для Проекта А.

У меня получилось, что NPV Проекта Б — 491,5 доллара.

Расчет NPV для проекта Б можно посмотреть в таблице и на рисунке со шкалой времени.

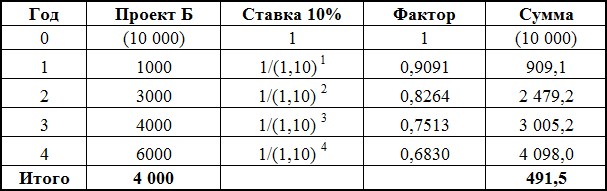
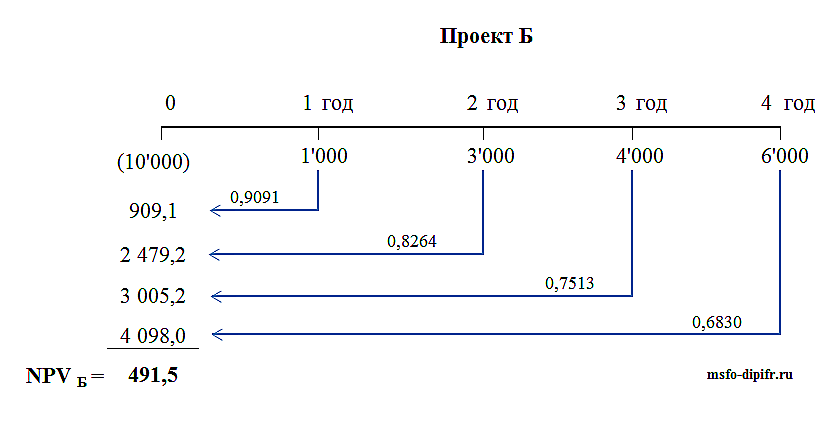
Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.

Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект А, поскольку его NPV заметно больше 788,2, чем NPV Проекта Б 491,5.

Цифры для расчета NPV инвестиционного проекта — в чём сложность?

Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала — то вы легко сможете подставить их в формулу и рассчитать NPV. Но не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.

а) Денежные потоки

Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.

Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.

Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.

б) Ставка дисконтирования

Ставка дисконтирования в формуле расчета NPV — это стоимость капитала (cost of capital) для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы.

В общем случае компания может получить финансирование из трех источников:

1. взять в долг (обычно у банка)
2. продать свои акции
3. использовать внутренние ресурсы (нераспределенную прибыль)

Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств (пункт 1 списка). Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.

Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC — сокращение по первым буквам английской фразы Weighted Average Cost of Capital, что переводится как средневзвешенная стоимость капитала.

Зависимость NPV проекта от ставки дисконтирования

Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала.

Давайте рассчитаем NPV по проектам А и Б для разных ставок дисконтирования. Я сделала этот расчет в Excele, результаты приведены в таблице ниже:

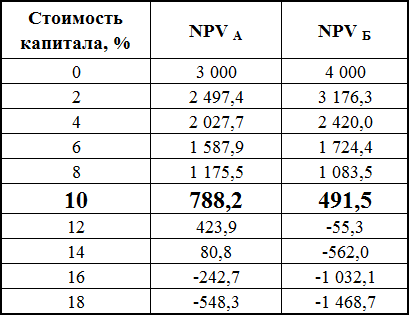
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):

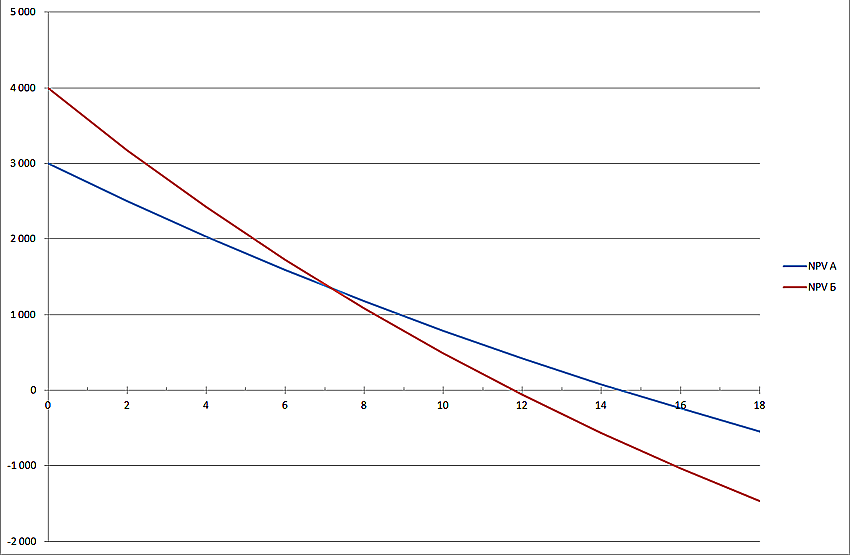
Из графика видно, что NPV проекта А превышает NPV проекта Б при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.

Кроме того, из графика также видно, что Проект Б (красная линия) является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта Б уменьшается ,быстрее по мере роста этой ставки (красный график более крутой). И это легко объяснимо. В проекте Б денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.

Например, можно рассчитать, чему будут равны 10,000 долларов через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения:

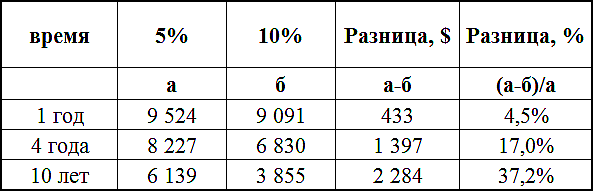
В последнем столбце таблицы видно, что один и тот же денежный поток (10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37,2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала (=ставка дисконтирования) «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать. Это математика.

Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.

История с выбором между двумя проектами А и Б будет продолжена в следующих публикациях на тему методов оценки инвестиционных проектов. К сожалению, большинство статей в Интернете на эту тему написано сухо и коротко, и многие из публикаций содержат ошибки, что недопустимо.

Расчет NPV — пример в Excel

В нашем компьютерном веке стало гораздо проще делать любые расчеты. В программе Excel есть функция, с помощью которой расчет NPV можно сделать быстрее, чем по таблицам. И не нужно дисконтировать каждый поток вручную. Проще зайти в раздел Excel Формулы —> Финансовые и выбрать функцию ЧПС.

Пример расчета NPV для проекта А показан ниже:

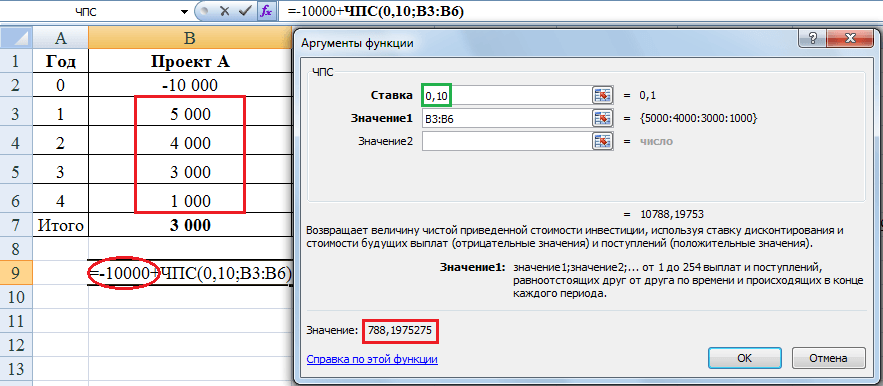
Единственная сложность заключается в том, что эта функция дисконтирует все потоки, которые вы выберете. Если же первый поток, как в проектах А и Б рассмотренных выше, приходится на период времени ноль, то его не надо вводить в ячейку значения. Первоначальная инвестиция в сумме -10,000 нужно добавить к тому значению, которое рассчитает функцию ЧПС. В этом примере дисконтируются ячейки B3-B6 (обведено красным в таблице), по ставке 0,10 (зеленый квадратик), приведенная стоимость получается равной 10,788.2. Если вычесть из этой суммы инвестицию 10,000, то получится NPV, равная 788,2. При расчете вручную мы получили 788,4, разница 0,2 получилась в результате округлений.

Другая функция программы Excel, расположенная в том же разделе финансовых формул, ЧИСТНЗ тоже считает приведенную стоимость денежных потоков, но она может это делать для неравных промежутков времени между потоками. В ней есть дополнительная ячейка, куда можно ввести диапазон дат, соответствующих времени поступления денежных средств.

И будет вам счастье и приличный счёт в банке.

Финансовая грамотность необходима каждому человеку. Современная экономика — это сложный механизм перекачивания денег из одного кармана в другой. И нужно не только научиться зарабатывать деньги, но и вкладывать их.

Учиться быть инвесторами желательно еще до того, как у вас появятся деньги. Если в будущем вам повезет, и вы выиграете миллион долларов в лотерею, то вы должны быть готовы к этому. Если вам удастся заработать достаточные для инвестирования средства, то тем более захочется распорядиться ими так, чтобы приумножить.

Источник http://capitalgains.ru/obrazovanie/chto-takoe-npv-i-kak-ego-rasschitat.html

Источник https://antiknik.ru/znaniya/chistaya-privedennaya-stoimost.html

Источник http://msfo-dipifr.ru/formula-rascheta-npv-investitsionnogo-proekta-eto-prosto/