Аргументы финансовых функций Excel анализа инвестиций
Рассмотрим функции Excel для расчета операций по кредитам, ссудам и займам. Эта группа функций обеспечивает решение следующих задач:
· определение наращенной суммы (будущей стоимости);
· определение начального значения (текущей стоимости);
· определение срока платежа и процентной ставки;
Отметим, что перед решением указанных задач следует ответить на два вопроса:
1. Кто является владельцем денежных средств? Например, в простой задаче накопления — вкладчик или банк? В задаче займа — должник или кредитор? При вычислении стоимости ряда будущих выплат — покупатель (выплата за приобретенный товар) или продавец (получение выплат за проданный товар)?
2. Как поступают денежные средства? Если денежные средства поступают к владельцу, то они имеют положительное значение, если уходят от владельца, то отрицательное.
Ответив на заданные вопросы, можно использовать финансовые функции Excel для проведения эффективных финансовых расчетов и правильно интерпретировать возвращаемые результаты.
Определение будущей стоимости на основе постоянной процентной ставки
Задача 1.
На банковский счет под 11,5% годовых внесли 37000 руб. Определить размер вклада по истечении 3 лет, если проценты начисляются каждые полгода.
Алгоритм решения задачи.
Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем функцию БС (ставка; кпер; плт; пс; тип). Опишем способы задания аргументов данной функции.
В связи с тем, что проценты начисляются каждые полгода, аргумент ставка равен 11,5%/2. Общее число периодов начисления равно 3*2 (аргумент кпер). Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада) равный 37 000 руб., задается в виде отрицательной величины (- 37 000), поскольку для вкладчика это отток его денежных средств (вложение средств). Если рассматривать решение данной задачи с точки зрения банка, то данный аргумент (пс) должен быть задан в виде положительной величины, т.к. означает поступление средств в банк.
Аргумент плт отсутствует, т.к. вклад не пополняется. Аргумент тип равен 0, т.к. в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Тогда к концу 3-го года на банковском счете имеем:
= БС (11,5%/2;3*2;;-37 000) = 51 746,86 руб., с точки зрения вкладчика это доход,
= БС (11,5%/2;3*2;;37 000) = — 51 746,86 руб., с точки зрения банка это расход, т.е. возврат денег банком вкладчику.
На практике, в зависимости от условий финансовой сделки проценты могут начисляться несколько раз в год, например, ежемесячно, ежеквартально и т.д. Если процент начисляется несколько раз в год, то необходимо определение общего числа периодов начисления процентов и ставки процента за период начисления. В таблице 4.3 приведены данные для наиболее распространенных методов внутригодового учета процентов.
Расчет данных для различных вариантов начисления процентов
| Метод начисления процентов | Общее число периодов начисления процентов | Процентная ставка за период начисления, % |
| Ежегодный | N | K |
| Полугодовой | N*2 | K/2 |
| Квартальный | N*4 | K/4 |
| Месячный | N*12 | K/12 |
| Ежедневный | N*365 | K/365 |
Этот же расчет можно выполнить по формуле:
где: Бс – будущая стоимость (значение) вклада;
Пс – текущая стоимость вклада;
Кпер – общее число периодов начисления процентов;
Ставка – процентная ставка по вкладу за период.
Подставив в формулу числовые данные, получим:
1. При аналитических вычислениях в Excel с помощью функций, связанных с аннуитетом, – БЗРАСПИС, БС, ОБЩДОХОД, ОБЩПЛАТ, ОСПЛТ, ПЛТ, ПРПЛТ, ПС, СТАВКА, ЧИСТВНДОХ, ЧИСТНЗ – используется следующее основное уравнение:
в котором наименования параметров Пс, Ставка, Кпер, Плт, Бс соответствуют описаниям из таблицы 4.2 (и, соответственно, одноименным встроенным функциям), а параметр Тип определяет обязательность выплаты платежей в начале периода (1) или выплату обычных платежей в конце периода (0).
2. Из уравнения (4.2) могут быть выражены значения бс, пс, ставка, кпер, плт через другие параметры. Эти выражения используются соответствующими функциями Excel.
3. Если ставка равна 0, вместо уравнения (4.2) используется уравнение:
4. Если формула (4.1) не предусматривает задание денежных потоков, идущих от клиента, со знаком минус, то в формулах (4.2) и (4.3) это учтено.
Нахождение решения задачи 1 по формуле (4.2) дает тот же результат. Иллюстрация решения приведена на рис. 4.1.
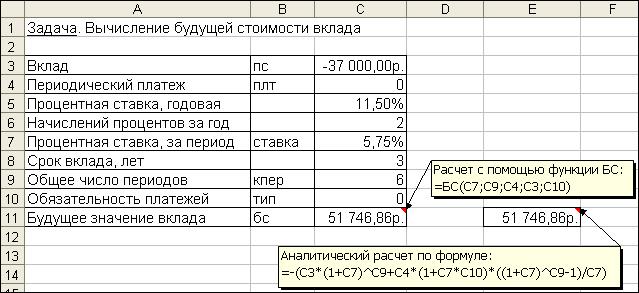
Рис. 4.1. Фрагмент листа Excel с решением задачи о нахождении будущего размера вклада
Задача 2 .
Определить, сколько денег окажется на банковском счете, если ежегодно в течение 5 лет под 17% годовых вносится 20 тыс. руб. Взносы осуществляются в начале каждого года.
Алгоритм решения задачи.
Поскольку следует рассчитать будущую стоимость фиксированных периодических выплат на основе постоянной процентной ставки, то воспользуемся функцией БС со следующими аргументами:
= БС(17%;5;-20000;;1) = 164 136,96 руб.
Если бы взносы осуществлялись в конце каждого года, результат был бы:
= БС(17%;5;-20000) = 140 288 руб.
В рассмотренной функции не используется аргумент пс, т.к. первоначально на счете денег не было.
Решение задачи может быть найдено с использованием формулы:
где: Бс – будущая стоимость потока фиксированных периодических платежей;
Плт – фиксированная периодическая сумма платежа;
Кпер – общее число периодов выплат;
Ставка – постоянная процентная ставка;
i – номер текущего периода выплаты платежа.
Результат аналитического вычисления:
Задача 3.
Достаточно ли положить на счет 85 000 руб. для приобретения через 5 лет легкового автомобиля стоимостью 160 000 руб.? Банк начисляет проценты ежеквартально, годовая ставка 12%.
Произвести расчеты при разных вариантах процентной ставки.
Алгоритм решения задачи.
Поскольку требуется найти будущее значение суммы вклада через 5 лет, для решения поставленной задачи воспользуемся функцией БС. Получим:
=БС(12%/4;5*4;;-85000; 0)= 153 519,45р.
Как видим, найденная сумма недостаточна для совершения покупки. Чтобы осуществить мечту, существует два варианта: первоначально положить на счет большую сумму или воспользоваться банком, где предусмотрена большая процентная ставка. Внесение дополнительных платежей рассматривать не будем.
Для определения необходимой суммы исходные данные задачи представим в виде таблицы и воспользуемся средством Подбор параметра из меню команды Сервис.
Иллюстрация решения представлена на рис. 4.2.
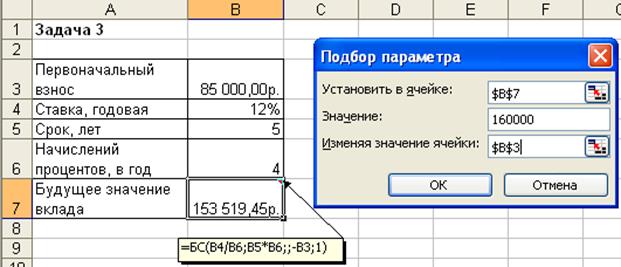
Рис. 4.2. Фрагмент окна Excel с заполненными полями подбора параметров
После подтверждения введенных данных в ячейке В7 установится значение 160 000,00р., а в ячейке B3 отобразится результат – 88 588,12р.
В данном случае также можно применить средство Подбор параметра из меню команды Сервис, изменяя ячейку, в которой находится процентная ставка. Однако для анализа влияния процентной ставки на зависящую от нее формулу расчета будущей суммы вклада воспользуемся другим средством – Таблицей подстановки из меню Данные.
В дополнение к исходным данным задачи, представленным в виде таблицы, наметим контуры будущей таблицы подстановки: укажем наименования столбцов, в ячейки D9:D16 введем процентные ставки (входы в нашу таблицу подстановки будут размещаться слева в строках), а в ячейку Е8 введем формулу расчета будущего значения единой суммы вклада. Затем выполним необходимые действия по инициализации средства Таблица подстановки и внесения в соответствующее поле подстановки по строкам значения адреса ячейки с процентной ставкой.
Иллюстрация окна Excel после задания параметров для таблицы подстановки, а также контрольные значения искомых результатов представлены на рис. 4.3.
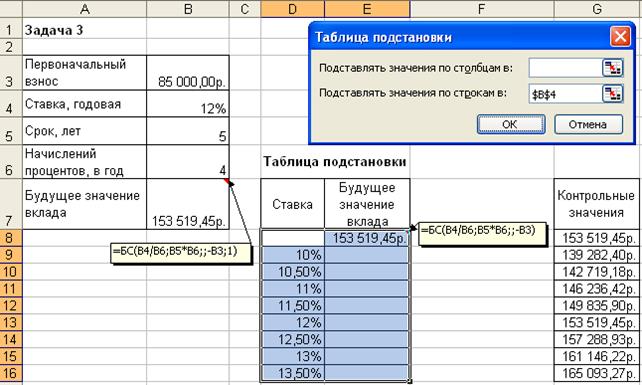
Рис. 4.3. Фрагмент окна Excel с заполненными полями таблицы подстановки
После подтверждения в диалоговом окне заданных параметров таблицы подстановки в диапазоне ячеек Е9:Е16 автоматически появятся результаты, полностью совпадающие с контрольными значениями.
Из результатов следует, что годовые ставки менее 13% не обеспечивают рост вклада до требуемой величины, равной 160 000 р.
При ставке 13% значение вклада вырастет до 161 146,22р., а ставка 13,5% обеспечивает рост вклада до 165 093,27р.
Определение будущей стоимости на основе переменной процентной ставки
Задача 1.
По облигации номиналом 50 000 руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10%, в следующие два года – 20%, в оставшиеся три года – 25%.
Определить будущую стоимость облигации с учетом переменной процентной ставки.
Алгоритм решения задачи.
Поскольку процентная ставка меняется со временем, но является постоянной на протяжении каждого из периодов одинаковой продолжительности, то для расчета будущего значения инвестиции по сложной процентной ставке следует воспользоваться функцией БЗРАСПИС (первичное; план).
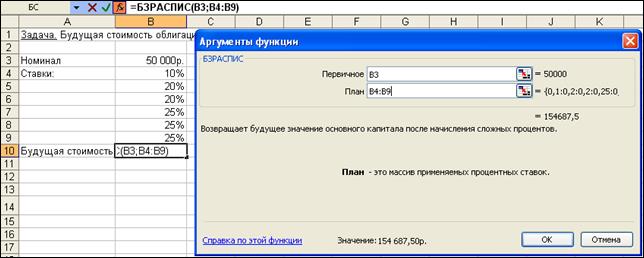
Иллюстрация решения задачи представлена на рис. 4.4.
Рис. 4.4. Окно функции БЗРАСПИС с данными о будущей стоимости облигации
Результат решения задачи – 154 687,50 р. может быть найден и при явной записи функции БЗРАСПИС. Массив процентных ставок в этом случае следует ввести в фигурных скобках:
Для вычислений будущей стоимости функция БЗРАСПИС использует следующую формулу:
где: Бзраспис – будущая стоимость инвестиции при переменной процентной ставке;
Пс – текущая стоимость инвестиции;
Кпер – общее число периодов;
Ставкаi – процентная ставка в i-й период.
Расчеты по указанной формуле дают тот же результат:
Задача 2.
По облигации, выпущенной на 6 лет, предусмотрен порядок начисления процентов, приведенный в задаче 1. Рассчитать номинал облигации, если известно, что ее будущая стоимость составила 154 687,50 руб.
Алгоритм решения задачи.
Для решения предложенной задачи воспользуемся аппаратом подбора параметра (из меню команды Сервис).
Пусть исходные данные задачи введены в соответствие с рис. 4.4: в ячейках В4:В9 набраны процентные ставки; ячейка В3 предназначена для хранения значения номинала облигации; в ячейку В10 введена формула =БЗРАСПИС(B3;B4:B9).
Инициируем процедуру подбора параметра (из меню команды Сервис) и заполним диалоговое окно в соответствие с данными, представленными на рис. 4.5.
После подтверждения ввода данных в результате подбора параметра в ячейке В3 получим значение номинала облигации – 50 000 р.
Задания для самостоятельной работы
1. В банк на депозит внесена сумма 30 тыс. руб. Срок депозита 2 года, годовая ставка – 12%. Начисление процентов производится ежеквартально. Определить величину депозита в конце срока.
2. Существует два варианта денежных вкладов по 50 тыс. руб. в течение трех лет: в начале каждого года под 19% годовых или в конце каждого года под 27% годовых. Определить наиболее предпочтительный вариант.
3. Два клиента банка в течение нескольких лет вносят одинаковые фиксированные денежные суммы под 14% годовых. Один клиент делает вклад в начале каждого квартала, другой – в конце каждого месяца. Определить размеры накопленных клиентами к концу пятого года сумм, если общая сумма взносов каждого из них за год равнялась 12 тыс. руб.
4. Определить величину вклада, если сумма размером 7 тыс. руб. помещена в банк под 11% годовых на 28 месяцев, а проценты начисляются ежеквартально.
5. По вкладу размером 3 тыс. руб. начисляется 13% годовых. Определить сумму вклада через 2 года, если проценты начисляются ежемесячно.
6. В начале каждого месяца на счет в банке вносится 1 тыс. руб. Определить накопленную за 3 года сумму вклада при ставке процента 13,5% годовых.
7. Банк принимает вклад на срок 3 месяца под 15% годовых или на 6 месяцев под 17% годовых. Как выгоднее вкладывать деньги на полгода: дважды на 3 месяца или один раз на 6 месяцев?
8. Выдан кредит в сумме 500 тыс. руб. на срок с 15 января по 15 марта текущего года под 15% годовых. Рассчитать сумму погасительного платежа.
9. Рассчитать будущую стоимость облигации номиналом 100 тыс. руб., выпущенной на 4 года, если предусмотрен следующий порядок начисления процентов: в первый год – 12,5%, в следующие два года – 14%, в последний год – 17% годовых.
10. Ожидается, что будущая стоимость инвестиции размером 150 тыс. руб. к концу четвертого года составит 300 тыс. руб. При этом за первый год доходность составит 15%, за второй – 17%, за четвертый – 23%. Рассчитать доходность инвестиции за третий год, используя аппарат подбора параметра.
11. Ставка банка по валютным вкладам на начало года составляет 10% годовых, начисляемых раз в квартал. Первоначальная сумма вклада 500 у.е. В течение года, в начале последующих кварталов, ожидается снижение ставки от первоначального размера на 2, 3 и 5 процентов соответственно. Определить величину вклада на начало следующего года.
12. Корпорация планирует ежеквартально в течение 8-ми лет делать отчисления по 2 000 руб. для создания фонда выкупа своих облигаций. Средства помещаются в банк под 10% годовых. Какая сумма будет накоплена к концу срока операции?
13. Клиент внес в банк вклад на сумму 5 тыс. руб. сроком на один год. Процентная ставка по вкладу в первом квартале составила 12% годовых, в середине второго квартала понизилась до 9%, в начале четвертого квартала снова возросла до 12% годовых. Какую сумму клиент получит в конце года?
14. Если Вы занимаете 30 000 рублей на два года под 8% годовых, то сколько всего денег Вы должны возвратить?
15. Если начальный баланс на счете 6 000 рублей и ежемесячный взнос 500 рублей (в конце каждого месяца), то сколько можно накопить за три года при ставке 0,75% в месяц?
16. Имеется возможность приобретения недвижимости, выплатив строго фиксированную сумму 1 500 000 руб. равномерными авансовыми месячными платежами по 15 000 руб. в течение некоторого периода. В дальнейшем, через 5 лет, недвижимость предполагается продать. Какой на этот момент должна быть ее цена, если планируется за весь срок получить доход, равный 1% в месяц?
17. Финансовая компания создает фонд для погашения обязательств путем помещения в банк суммы в 60 000 руб., с последующим ежегодным пополнением суммами по 10 000 руб. Ставка по депозиту равна 12% годовых. Какова будет величина фонда к концу 6-го года?
Определение текущей стоимости
Часто в расчетах используется понятие текущей стоимости будущих доходов и расходов, связанное с концепцией временной стоимости денег. Согласно этой концепции платежи, осуществленные в различные моменты времени, можно сопоставлять (сравнивать, складывать, вычитать) лишь после приведения их к одному временному моменту.
Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени. Функции Excel, относящиеся к данной теме – ПС (ставка; кпер; плт; бс; тип), ЧПС (ставка; значения), ЧИСТНЗ (ставка; значения; даты).
Функция ПС используется, если денежный поток представлен в виде серии равных платежей, осуществляемых через равные промежутки времени.
Функция ЧПС применяется, если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени.
Функция ЧИСТНЗ применяется, если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени.
Задача 1.
Фирме требуется 500 тыс. руб. через три года. Определить, какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500 тыс. руб., если процентная ставка составляет 12% годовых.
Алгоритм решения задачи.
Для расчета суммы текущего вклада зададим исходные данные в виде таблицы. При вводе формулы вызовем функцию ПС и в полях ее панели укажем адреса требуемых параметров (рис. 4.6). В результате вычислений получим отрицательное значение, так как указанную сумму фирме потребуется внести.
При непосредственном вводе данных получается то же значение вклада:
= ПС (12%; 3; ; 500000) = — 355 890,12 руб.
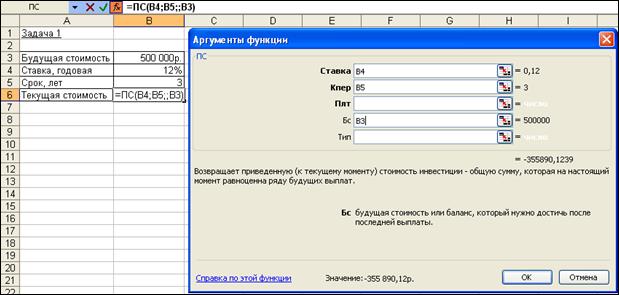
Рис. 4.6. Фрагмент окна Excel с панелью функции ПС
Напомним, что расчет текущей стоимости с помощью функции ПС является обратным к определению будущей стоимости с помощью функции БС (см. формулы (4.1) и (4.2)). Расчет производится путем дисконтирования по ставке сложных процентов, используя формулу:
Формула (4.6) дает аналогичный результат решения задачи, но, базируясь на формуле (4.1), не учитывает знак минус для денежных потоков от клиента:
Вычисления на основе уравнения (4.2) дают полностью правильный результат.
Задача 2.
Клиент заключает с банком договор о выплате ему в течение 5 лет ежегодной ренты в размере 5 тыс. руб. в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20%?
Алгоритм решения задачи.
Для расчета настоящего объема предполагаемой инвестиции на основе постоянных периодических выплат в размере 5 тыс. руб. в течение 5 лет используется функция ПС. Подставив исходные данные в заданную функцию, получим:
= ПС( 20%; 5; 5000; 0; 0) = -14 953,06 руб.
Знак «минус» означает, что клиент должен вложить 14953,06 руб., чтобы потом получить выплаты.
Расчет текущей стоимости серии будущих постоянных периодических выплат, производимых в конце периода (обычные платежи) и дисконтированных нормой дохода ставка, ведется по формуле:
где: Пс – текущая стоимость серии фиксированных периодических платежей;
Плт – фиксированная периодическая сумма платежа;
Кпер – общее число периодов выплат (поступлений);
Ставка – постоянная процентная ставка.
Вычисления по формуле (4.7) дают то же значение (без учета знака):
Задача 3.
Пусть инвестиции в проект к концу первого года его реализации составят 20 000 руб. В последующие четыре года ожидаются годовые доходы по проекту: 6 000 руб., 8 200 руб., 12 600 руб., 18 800 руб.
Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10% годовых.
Алгоритм решения задачи.
Чистая текущая стоимость проекта для периодических денежных потоков переменной величины рассчитывается с помощью функции ЧПС.
Так как по условию задачи инвестиция в сумме 20 000 руб. вносится к концу первого периода, то это значение следует включить в список аргументов функции ЧПС со знаком «минус» (инвестиционный денежный поток движется «от нас»). Остальные денежные потоки представляют собой доходы, поэтому при вычислениях укажем их со знаком «плюс».
Иллюстрация решения задачи представлена на рис. 4.7.
Чистая текущая стоимость проекта к началу первого года составляет:
= ЧПС (10%; -20000; 6000; 8200; 12600; 18800) = 13 216,93 руб.
Данный результат представляет собой чистую прибыль от вложения 20 тыс. руб. в проект с учетом покрытия всех расходов.
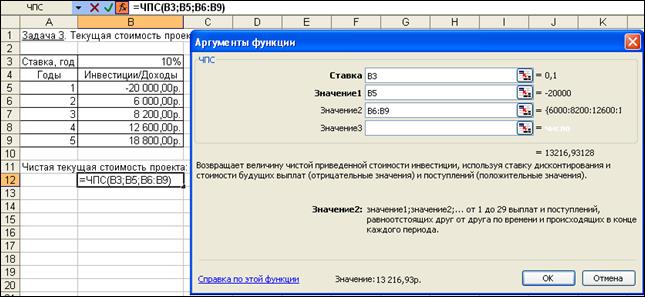
Рис. 4.7. Фрагмент окна Excel с панелью функции ЧПС
При расчете чистой приведенной стоимости инвестиций с помощью функции ЧПС учитываются периодические платежи переменной величины как суммы ожидаемых расходов и доходов в каждый из периодов, дисконтированные нормой процентной ставки, с использованием следующей формулы:
где: ЧПС – чистая текущая стоимость периодических выплат и поступлений;
Значениеi – суммарный размер i-го денежного потока на конец периода (поступления – со знаком «плюс», выплаты – со знаком «минус»);
Ставка – норма дисконтирования за один период;
n – число периодов движения денежных потоков (суммарное количество выплат и поступлений);
i – номер периода денежного потока.
Аналитический расчет задачи дает аналогичный результат:
Задача 4.
Инвестор с целью инвестирования рассматривает 2 проекта, рассчитанных на 5 лет. Проекты характеризуются следующими данными:
· по 1-му проекту – начальные инвестиции составляют 550 тыс. руб., ожидаемые доходы за 5 лет соответственно 100, 190, 270, 300 и 350 тыс. руб.;
· по 2-му проекту – начальные инвестиции составляют 650 тыс. руб., ожидаемые доходы за 5 лет соответственно 150, 230, 470, 180 и 320 тыс. руб.
Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15% годовых.
Алгоритм решения задачи.
Оценку привлекательности проектов выполним с помощью показателя чистой текущей стоимости (функции ЧПС).
Поскольку оба проекта предусматривают начальные инвестиции, вычтем их из результата, полученного с помощью функции ЧПС. (Начальные инвестиции по проекту не нужно дисконтировать, так как они являются предварительными, уже совершенными к настоящему моменту времени).
Для облегчения анализа полученного решения исходные данные задачи представим в виде таблицы и в соответствующие ячейки введем значения формул с функциями ЧПС (рис. 4.8). В результате вычислений получим, что чистая приведенная стоимость инвестиций во второй проект почти на 22 тыс. руб. выше, чем в первый.
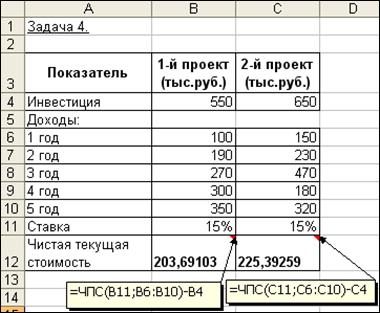
Непосредственное задание параметров в формулах расчета, как и вычисления с использованием формулы (4.8), дают те же результаты.
Для первого проекта:
= ЧПС (15%; 100000; 190000; 270000; 300000; 350000) – 550000 = 203 691,03р.
Для второго проекта:
= ЧПС (15%; 150000; 230000; 470000; 180000; 320000) – 650000 = 225 392,59р.
Таким образом, второй проект является для инвестора более привлекательным.
В некоторой степени функции ПС и ЧПС похожи. Сравнивая их, можно сделать следующие выводы:
1) в функции ПС периодические выплаты предполагаются одинаковыми, а в функции ЧПС они могут быть различными;
2) в функции ПС платежи и поступления происходят как в конце, так и в начале периода, а в функции ЧПС предполагается, что все выплаты производятся равномерно и всегда в конце периода.
Из последнего вывода следует, что если денежный взнос осуществляется в начале первого периода, то его значение следует исключить из аргументов функции ЧПС и добавить (вычесть, если это затраты) к результату функции ЧПС. Если же взнос приходится на конец первого периода, то его следует задать в виде отрицательного первого аргумента массива значений функции ЧПС.
Нельзя непосредственно оценивать эффективность, например, с помощью функции ЧПС, нескольких инвестиционных проектов, имеющих разную продолжительность. Предполагая, что допускается реинвестирование, необходимо свести полученные результаты чистой текущей стоимости по каждому из них к единому по продолжительности периоду. С этой целью можно воспользоваться специальными методами.
Метод цепного повтора предполагает оценку эффективности проектов в рамках общего одинакового срока их действия. Находится наименьшее общее кратное продолжительности проектов и рассчитывается, сколько раз каждый из них должен повториться. Затем определяется с учетом повторов и реинвестирования чистая приведенная стоимость каждого из проектов, которая и сравнивается. Большему значению соответствует более привлекательный проект.
Суммарная чистая приведенная стоимость повторяющегося потока для каждого из проектов находится по формуле:
где: ЧПС(n) – чистая приведенная эффективность исходного проекта, найденная с учетом предварительных инвестиций;
n – длительность исходного проекта;
i – число повторов исходного проекта;
Ставка – норма дисконтирования за один период.
Метод бесконечного цепного повтора предполагает, что каждый из проектов может быть реализован неограниченное число раз.
Задача 5.
Сравнить инвестиционную привлекательность двух проектов. Цена капитала составляет 10%. Предварительные инвестиции в первый проект составляют 100 млн. руб., во второй – 105 млн. руб. Продолжительность первого проекта – 2 года; доходы по годам – 50 и 70 млн. руб. соответственно. Продолжительность второго проекта – 3 года; доходы по годам – 34, 40 и 60 млн. руб. соответственно.
Алгоритм решения задачи.
Для решения задачи предварительно рассчитаем чистую приведенную стоимость проектов при их однократном выполнении, воспользовавшись функцией ЧПС и вычтя предварительные инвестиции. Затем, принимая во внимание разную продолжительность проектов, рассчитаем значения эффективности проектов по формулам (4.9) и (4.10).
При однократном выполнении проектов предпочтительным выходит второй проект (ЧПС1 = 3,306; ЧПС2 = 4,046). Но такой вывод преждевременный (рис. 4.9).
Расчет эффективности проектов за 6 лет, а также при их бесконечном повторении дает результат полностью противоположный – более привлекательным является первый проект:
Задача 6.
Определить чистую текущую стоимость по проекту на 5.04.2005 г. при ставке дисконтирования 8%, если затраты по нему на 5.08.2005 г. составят 90 млн. руб., а ожидаемые доходы в течение следующих месяцев будут:
10 млн. руб. на 10.01.2006 г.;
20 млн. руб. на 1.03.2006 г.;
30 млн. руб. на 15.04.2006 г.;
40 млн. руб. на 25.07.2006 г.
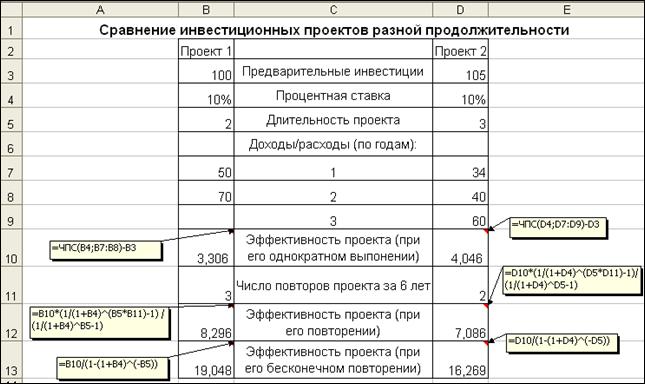
Рис. 4.9. Иллюстрация оценки эффективности инвестиционных проектов разной продолжительности
Алгоритм решения задачи.
Поскольку в данном случае имеем дело с нерегулярными переменными расходами и доходами, для расчета чистой текущей стоимости по проекту на 5.04.2005 г. необходимо применить функцию ЧИСТНЗ.
Расчет чистой текущей стоимости нерегулярных переменных расходов и доходов с помощью функции ЧИСТНЗ осуществляется по формуле:
где: Чистнз – чистая текущая стоимость нерегулярных переменных выплат и поступлений;
Ставка – норма дисконтирования;
d1 – дата 0-й операции (начальная дата);
n – количество выплат и поступлений.
Для нахождения решения задачи предварительно построим таблицу с исходными данными. Рассчитаем рядом в столбце число дней, прошедших от начальной даты до соответствующей выплаты. Затем найдем требуемый результат – с помощью функции ЧИСТНЗ и по формуле (4.11). Получим значение – 4 267 559 руб. 31 коп. Иллюстрация решения приведена на рис. 4.10.
Непосредственный ввод параметров в ЧИСТНЗ дает тот же результат:
=ЧИСТНЗ (8%;; B4:B8) = 4,26755931 млн. руб.
Вычисление решения задачи по формуле (4.11):
1. При явной форме записи функции ЧИСТНЗ нельзя непосредственно указывать в каком бы то ни было допустимом формате массив дат в качестве ее параметров. Обязательно следует ссылаться на ячейки, где эти даты приведены.
2. Аналитические вычисления по формулам следует выполнять на листе Excel (а не на калькуляторе).
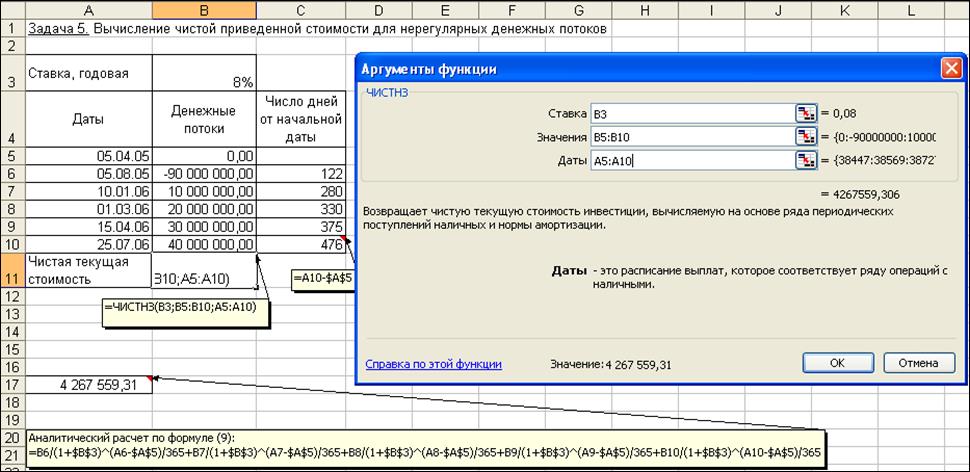
Рис. 4.10. Иллюстрация примера использования функции ЧИСТНЗ
Задания для самостоятельной работы
| Показатели | Проект 1 | Проект 2 |
| Инвестиции | ||
| Доходы: | ||
| 1 год | ||
| 2 год | ||
| 3 год |
1. Определить, какой из двух представленных проектов является наиболее привлекательным для инвестора. Ставка банковского процента составляет 13% годовых. Другие данные о проектах приведены в таблице.
2. Определить чистую текущую стоимость проекта, если ставка дисконтирования равна 12%. Проект требует начальных инвестиций в размере 5 млн. руб. Предполагается, что в конце 1 года убыток составит 900 тыс. руб., а в следующие 3 года ожидается доход в размере: 1 500 тыс. руб., 3 200 тыс. руб. и 3 800 тыс. руб. соответственно.
Рассчитать также чистую текущую стоимость проекта при условии, что убыток в конце 1 года будет 1 100 тыс. руб.
3. Дать заключение по инвестиционному проекту для 5-ти регионов, если известно, что:
| Год | Доходы | Расходы |
| — | ||
| — |
· проект рассчитан на 5 лет;
· ставка дисконтирования по 1-му региону составляет 5%, по 2-му – 6%, по 3-му – 7%, по 4-му – 8%, по 5-му – 9%.
· Другие данные о проекте приведены в таблице.
Задачу следует решать, используя средство Таблица подстановки из меню команды Данные. Результаты представить в графическом виде.
4. В инвестиционную компанию для рассмотрения поступили два различных по продолжительности инвестиционных проекта. Предполагаемые данные о проектах приведены в таблице. Необходимо:
· сравнить проекты и выбрать наиболее эффективный из них;
· проанализировать проекты при одинаковых объемах инвестируемых средств.
| Проект 1 | Проект 2 | ||
| Ставка дисконтирования | 9% | Ставка дисконтирования | 11% |
| Объем инвестиций | 120 тыс. руб. | Объем инвестиций | 100 тыс. руб. |
| Годы: | Денежный поток (тыс. руб.) | Годы: | Денежный поток (тыс. руб.) |
5. Рассматриваются два варианта покупки недвижимости. Первый вариант предполагает единовременную оплату в размере 700 тыс. руб. Второй вариант рассчитан на ежемесячную оплату по 9 тыс. руб. в течение 13 лет.
· Определить, какой вариант является более выгодным, если ставка процента равна: а) 10% годовых; б) 13% годовых.
· Рассчитать сумму ежемесячных взносов при ставке 10% годовых, чтобы второй вариант являлся более предпочтительным.
6. Определить текущую стоимость обязательных ежеквартальных платежей размером 80 тыс. руб. в течение 7 лет, если процентная ставка составляет 15% годовых.
7. Рассчитать суммы, которые необходимо положить на депозит для того, чтобы через 6 лет получить 10 млн. руб. при различных вариантах начисления процентов: ежемесячном, ежеквартальном, полугодовом и годовом. Процентная ставка – 11% годовых.
8. Предприниматель получил в банке кредит под 12% годовых. Какова текущая стоимость кредита, если предприниматель должен в течение 7 лет перечислять в банк по 253 000 руб. ежегодно?
9. Рассчитать чистую текущую стоимость проекта, если:
· к концу первого года его инвестиции составят 34 тыс. руб., а ожидаемые доходы в последующие годы соответственно будут: 5 тыс. руб., 17 тыс. руб. и 25 тыс. руб.; годовая учетная ставка – 12%;
· решить задачу с теми же условиями, но с учетом предварительной инвестиции в проект 10 тыс. руб.;
· проанализировать получаемую чистую текущую стоимость проекта при различных первоначальных объемах инвестиций и разных процентных ставках.
10. Для приобретения квартиры молодая семья планирует в дополнение к собственным накоплениям в размере $12 000 взять в банке ипотечный кредит сроком на 20 лет под 11,5% годовых. Ежемесячно семья может выплачивать по кредиту не более $700.
· На какой кредит может рассчитывать семья? Какой может быть стоимость приобретаемой квартиры?
· Какой может быть стоимость приобретаемой квартиры, если взять в банке кредит с другими условиями: а) на 10 лет под 10,5% годовых; б) на 15 лет под 11% годовых?
· Используя команду Таблица подстановки, рассчитать возможную стоимость приобретаемой квартиры: а) при различных размерах собственных накоплений и разных сроках действия кредита; б) при различных ежемесячных платежах по кредиту и разных сроках его действия.
11. У Вас на депозитном счету 10 570,5 рублей, положенные под 1% ежемесячно. Счет открыт 12 месяцев назад. Каков был начальный вклад?
12. Ежегодная плата за приобретенную недвижимость на следующие 25 лет составляет 25 000 рублей. Если считать покупку недвижимости займом с 8% годовых, то какой должна быть его величина, чтобы рассчитаться с займом через 25 лет?
13. Если использовать учетную ставку 0,75% в месяц, сколько необходимо выплатить вначале за имущество, которое по оценке будет стоить 5 000 000 рублей? Ежемесячная плата составляет 25 000 рублей в течение пяти лет.
14. Вы можете позволить себе ежемесячные выплаты 2 500 рублей со ставкой 0,45% (в месяц) в течение 20 лет. Сколько можно занять, чтобы полностью погасить заем?
Определение срока платежа и процентной ставки
В ходе решения задач, связанных с аннуитетом, общее количество периодов выплаты определяется с помощью функции КПЕР (ставка; плт; пс; бс; тип). Процентная ставка за период вычисляется с применением функции СТАВКА (кпер; плт; пс; бс; тип; предположение).
Задача 1.
Рассчитать, через сколько лет вклад размером 100 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 13,5% годовых и начисление процентов производится ежеквартально.
Алгоритм решения задачи.
При квартальном начислении процентов ставка процента за период начисления равна 13%/4. Чтобы определить общее число периодов выплат для единой суммы вклада, воспользуемся функцией КПЕР со следующими аргументами: ставка= 13%/4; пс= -1; бс = 10. Нули в текущей и будущей суммах можно не набирать, достаточно сохранить между ними пропорции.
Значением функции КПЕР является число периодов, необходимое для проведения операции, в данном случае — число кварталов. Для нахождения числа лет полученный результат разделим на 4:
= КПЕР (13%/4;;-1;10) / 4 = 18
Иллюстрация решения задачи приведена на рис. 4.11.
Для решения задачи можно также воспользоваться формулой (4.1), в которой аргумент Кпери есть значение функции КПЕР. Выполнив преобразования и прологарифмировав обе части уравнения (4.1), получим:
Подставив в (4.12) значения, убедимся в совпадении результатов:
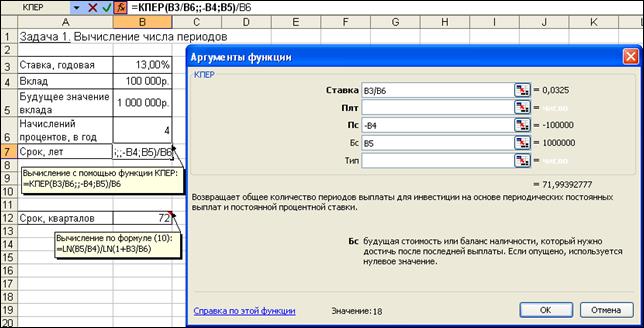
Рис. 4.11. Иллюстрация применения функции КПЕР и аналитической формулы для вычисления числа периодов
Задача 2 .
Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Сумма разового платежа 16 000 руб. На поступившие взносы начисляются 11,2% годовых. Необходимо определить, когда величина фонда будет равна 100 000 руб.
Алгоритм решения задачи.
Для определения общего числа периодов, через которое будет достигнута нужная сумма, воспользуемся функцией КПЕР с аргументами: ставка = 11,2%; плт = -16; бс = 100. В результате вычислений получим, что через 5 лет величина фонда достигнет отметки 100 000 руб.:
= КПЕР (11,2%;-16;;100) = 5
Решение задачи может быть найдено и иным способом – с помощью функций БС (либо ПС) и последующего подбора параметра.
Иллюстрация решения приведена на рис. 4.12.
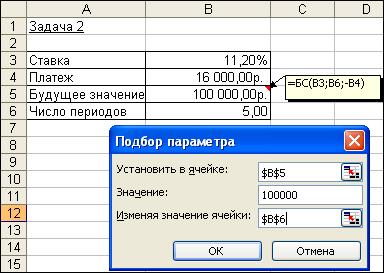
Рис. 4.12. Применение функции БС и механизма подбора параметра для определения числа периодов
Задача 3.
Предположим, что для получения через 2 года суммы в 1 млн. руб. предприятие готово вложить 250 тыс. руб. сразу и затем каждый месяц по 25 тыс. руб. Определить годовую процентную ставку.
Алгоритм решения задачи.
В данной задаче сумма в 1 млн. руб. формируется за счет приведения к будущему моменту времени начального вклада 250 тыс. руб. и фиксированных ежемесячных выплат.
Определим значение процентной ставки за месяц с помощью функции СТАВКА, имеющей аргументы: Кпер= 2*12 = 24 (месяца);Плт= -25; Пс= -250; Бс= 1000. Тогда:
= СТАВКА (24;-25;-250;1000) = 1,05%
Для вычисления годовой процентной ставки значение, выданное функцией СТАВКА, следует умножить на 12: 1,05%*12 = 12,63%. Процент на вклад должен быть не меньше этой величины.
Иллюстрация применения функции СТАВКА в выражениях формулы приведена на рис. 4.13.
Обратим внимание, что функция СТАВКА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений.
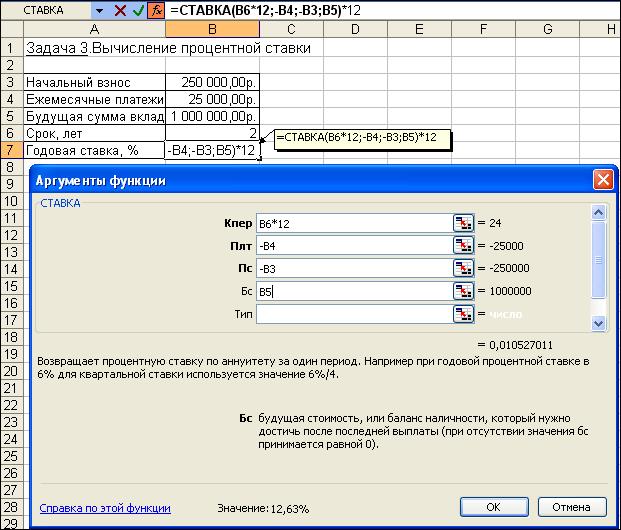
Рис. 4.13. Фрагмент экрана при использовании функции СТАВКА
Сначала рассчитывается текущий объем инвестиции при ставке, задаваемой аргументом функции СТАВКА предположение,по умолчанию равным 10%.Если результат получается больше 0, то значение процентной ставки увеличивается, и расчет текущего объема инвестиции повторяется. Если результат оказывается меньше 0, то для следующего приближения значение процентной ставки уменьшается. Процесс завершается, когда решение получится с точностью до 0,0000001 или когда количество итераций превысит 20. В последнем случае считается, что решения нет (формируется ошибка #ЧИСЛО!), и для повторного поиска решения следует изменить значение аргумента предположение (рис. 4.14). Это можно сделать, до бавив его значение из интервала между 0 и 1 в строке формул или, сдвинув ползунок в панели функции СТАВКА, в появившейся строке ввести новое значение аргумента предположение.
1. Следует помнить, что результатами функций КПЕР и СТАВКА являются число периодов и периодическая процентная ставка текущей операции, поэтому для годовых результатов требуются преобразования.
2. Следует также помнить, что для получения корректного результата при работе с функциями КПЕР и СТАВКА, аргументы Бс и Пс должны иметь противоположные знаки. Данное требование вытекает из экономического смысла подобных операций.
Задания для самостоятельной работы
1. Ссуда размером 58 000 руб., выданная под 12% годовых, погашается ежеквартальными платежами по 6 200 руб. Рассчитайте срок погашения ссуды.
2. Предполагается, что ежегодные доходы от реализации проекта составят 30 млн. руб. Рассчитать срок окупаемости проекта, если затраты по проекту к началу поступления доходов составят 70 млн. руб., а норма дисконтирования – 11,3%.
3. Вычислите, через сколько лет ежемесячные взносы в сумме 15 000 руб. принесут доход в 500 000 руб. при ставке процента 11,9% годовых.
4. Какой вариант инвестиций из трех предпочтительнее по сроку окупаемости? Варианты инвестиций характеризуются потоками платежей, приведенными в таблице (в тыс. руб.).
| Вариант | Начальные затраты | Ежегодные поступления |
| -200 | ||
| -270 | ||
| -330 |
5. Пусть в долг на 3,5 года дана сумма 1 000 тыс. руб. с условием возврата 1500 тыс. руб. Определить, под какой процент годовых одолжена сумма?
6. Выдан кредит 500 тыс. руб. на 2,5 года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 700 тыс. руб.
7. Вычислить процентную ставку для трехлетнего займа размером 3 млн. руб. с ежеквартальным погашением по 300 тыс. руб.
8. Клиент внес в банк 10 000 руб. и к концу года рассчитывает на 15 000 руб. Проценты начисляются ежемесячно. Определить процентную ставку по вкладу.
9. Кредит в 750 тыс. руб. предоставлен под 12% годовых и предусматривает ежемесячные платежи в размере 8632,5 руб. Определить срок погашения кредита.
10. Ваш остаток на счете пять лет назад составлял 25 000 рублей. В конце каждого года Вы добавляли 4500 рублей. Сегодня баланс равен 70 000 рублей. Какой была Ваша среднегодовая ставка?
11. Имущество с текущей стоимостью 2 000 000 рублей продается в кредит с обязательством погашения кредита в течение пяти лет. Покупатель оплатил 1 850 000 рублей. Не принимая во внимание рост стоимости имущества, определите начальную ставку?
12. Вы заплатили 1 500 000 рублей за имущество, внося ежемесячно по 15 000 рублей. Если Вы продадите имущество через пять лет за 1 900 000 рублей, какой процент сможете получить?
13. Соглашение о потребительском займе предоставляет Вам кредит 10 000 рублей с оплатой 2 000 рублей в месяц в течение 12 месяцев. Какова его процентная ставка?
Расчет эффективной и номинальной ставки процентов
Часто на практике возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов. В этом случае осуществляют приведение соответствующих процентных ставок к их годовому эквиваленту.
Реальная доходность финансового контракта с начислением сложных процентов несколько раз в год измеряется эффективной процентной ставкой, которая показывает, какой относительный доход был бы получен за год от начисления процентов.
Зная эффективную процентную ставку, можно определить величину соответствующей ей годовой номинальной процентной ставки.
Для расчетов указанных величин используются функции – НОМИНАЛ (эффективная_ставка; кол_пер) и ЭФФЕКТ (номинальная_ставка; кол_пер).
Задача 1.
Определить эффективную процентную ставку, если номинальная ставка составляет 9%, а проценты начисляются:
а) раз в полгода;
Алгоритм решения задачи.
Для определения эффективной процентной ставки воспользуемся функцией ЭФФЕКТ. Непосредственный ввод аргументов дает следующие значения:
| а) = ЭФФЕКТ (9%; 2) = 9,2%, | в) = ЭФФЕКТ (9%; 12) = 9,38%. |
| б) = ЭФФЕКТ (9%; 4) = 9,31% |
Расчет эффективной ставки выполняется по формуле:
где Кол_пер – количество периодов в году, за которые начисляются сложные проценты.
Выполнив расчет по формуле (4.13), получим тот же результат. В качестве примера приведем вычисления для варианта б).
Иллюстрация решения с помощью панели функции приведена на рис. 4.15.
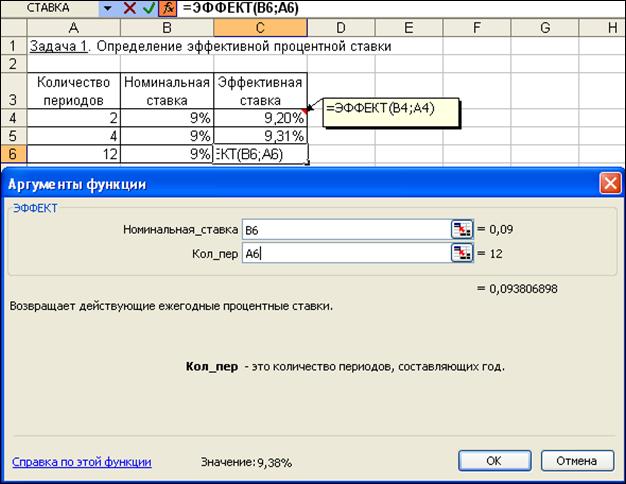
Рис. 4.15. Фрагмент окна при использовании функции ЭФФЕКТ
2. Если функция недоступна или возвращает ошибку #ИМЯ?, следует загрузить надстройку «Пакет анализа».
Задача 2.
Известно, что эффективная ставка составляет 16%, начисления производятся ежемесячно.
Определить номинальную ставку.
Алгоритм решения задачи.
Для определения номинальной годовой процентной ставки воспользуемся функцией НОМИНАЛ:
= НОМИНАЛ (16%; 12) = 14,93%.
Значение функции НОМИНАЛ – это аргумент Номинальная_ставка в формуле (4.13).
Задания для самостоятельной работы
1. Определить эффективную ставку, если номинальная ставка 10% и начисления процентов осуществляются:
| а) 5000 раз в год; | б) ежедневно. |
2. Эффективная ставка составляет 12%. Проценты начисляются ежеквартально. Определить номинальную ставку.
3. Ставка банка по срочным валютным депозитам составляет 20% годовых. Какова реальная доходность вклада, если проценты выплачиваются:
Расчет периодических платежей, связанных с погашением займов
Среди финансовых функций Excel выделяются функции, связанные с периодическими выплатами:
ПЛТ (ставка; кпер; пс; бс; тип)
ПРПЛТ (ставка; период; кпер; пс; бс; тип)
ОБЩПЛАТ (ставка; кол_пер; нз; нач_период; кон_период; тип)
ОСПЛТ (ставка; период; кпер; пс; бс; тип)
ОБЩДОХОД (ставка; кол_пер; нз; нач_период; кон_период; тип)
Задача 1.
Клиенту банка необходимо накопить 200 тыс. руб. за 2 года. Клиент обязуется вносить в начале каждого месяца постоянную сумму под 9% годовых.
Какой должна быть эта сумма?
Алгоритм решения задачи.
Для определения ежемесячных выплат применяется функция ПЛТ с аргументами: Ставка = 9%/12 (ставка процента за месяц); Кпер= 2*12 = 24 (общее число месяцев начисления процентов); Бс= 200 (будущая стоимость вклада); Тип= 1, так как вклады пренумерандо.
Тогда величина ежемесячных выплат равна:
= ПЛТ (9%/12; 24; ; 200; 1) = — 7,58 тыс. руб.
Результат со знаком «минус», так как 7,58 тыс. руб. клиент ежемесячно вносит в банк.
Иллюстрация решения задачи приведена на рис. 4.16.
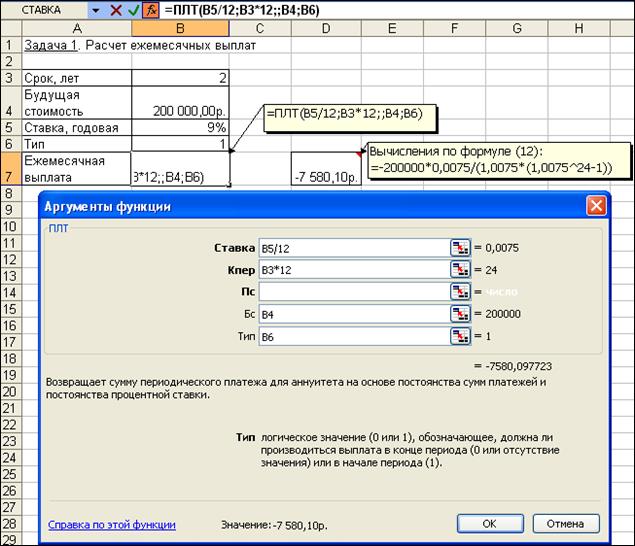
Рис. 4.16. Иллюстрация применения функции ПЛТ
Выплаты, определяемые функцией ПЛТ, включают основные платежи и платежи по процентам. Расчет выполняется по формуле, определяемой из (4.2):
Расчет задачи по формуле (4.12) дает тот же результат:
Задача 2.
Клиент банка осуществляет заем в размере 5000 руб. под 6% годовых на 6 месяцев. Определить ежемесячные платежи клиента. Платежи осуществляются в конце месяца.
Алгоритм решения задачи.
Для определения ежемесячных платежей клиента воспользуемся функцией ПЛТ, а также выполним расчет по формуле (4.14):
= ПЛТ (6%/12; 6; -5000) = 847,98 руб.
Отметим, что для банка выданный кредит – это отрицательная величина, а рассчитанные ежемесячные поступления от клиента – положительная величина.
Задача 3.
Определить платежи по процентам за первый месяц от трехгодичного займа в 100 000 руб. из расчета 10% годовых.
Алгоритм решения задачи.
Для определения платежа по процентам за первый месяц заданного периода применим функцию ПРПЛТ со следующими аргументами: Ставка= 10%/12 (процентная ставка за месяц); Период= 1 (месяц); Кпер = 3*12 = 36 (месяцев), Пс = 100 000 (величина займа). Тогда платежи по процентам за первый месяц составят:
= ПРПЛТ (10%/12; 1; 36; 100000) = — 833,33 руб.
Знак «минус» означает, что платеж по процентам необходимо внести.
Иллюстрация решения задачи приведена на рис. 4.17.
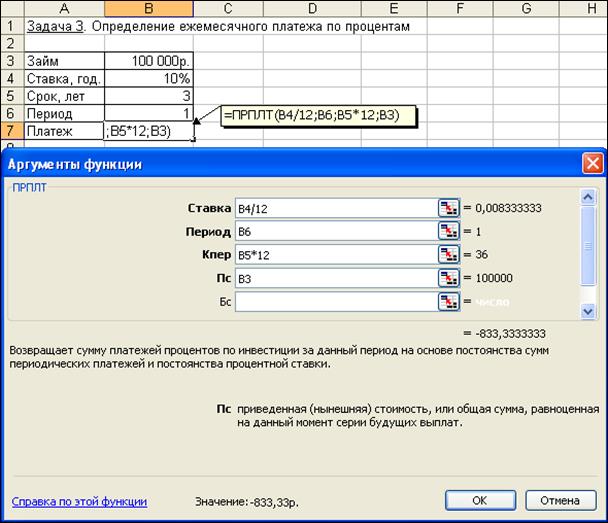
Рис. 4.17. Фрагмент окна с использованием функции ПРПЛТ
Задача 4.
Клиент ежегодно в течение 5 лет вносил деньги на свой счет в банке и накопил 40 000 руб.
Определить, какой доход получил клиент банка за последний год, если годовая ставка составила 13,5%.
Алгоритм решения задачи.
Доход за последний пятый год представляет собой сумму процентов, начисленных на накопленную сумму вложений.
Для расчета воспользуемся функцией ПРПЛТ:
= ПРПЛТ(13,5%; 5; 5; ; 40000) = 4030,77 руб.
Заметим, что при решении данной задачи значения аргументов функции ПРПЛТ Бс и Тип не указываются (считаются равными 0).
Задача 5.
Определить значение основного платежа для первого месяца двухгодичного займа в 60000 руб. под 12% годовых.
Алгоритм решения задачи.
Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ:
= ОСПЛТ (12%/12; 1; 24; 60000) = — -2 224,41руб.
Иллюстрация решения показана на рис. 4.18.
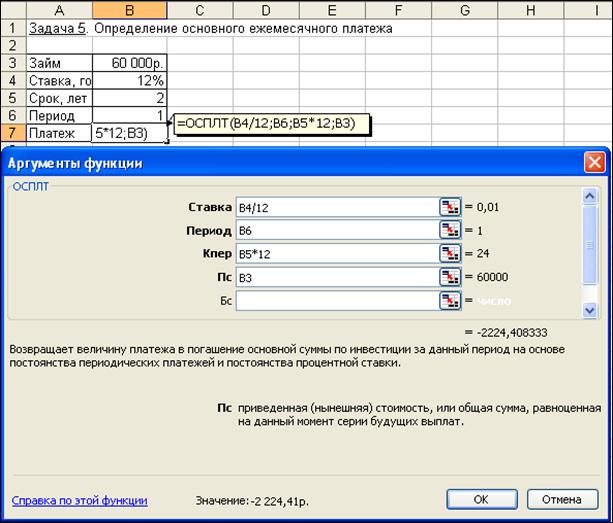
Рис. 4.18. Фрагмент окна с использованием функции ОСПЛТ
Знак «минус» в результате означает, что сумму основного долга по займу необходимо внести.
Отметим, что сумма выплаты по процентам, вычисляемая с помощью функции ПРПЛТ, и сумма основной выплаты за период, рассчитанная с помощью функции ОСПЛТ, равны полной величине выплаты, вычисляемой с помощью функции ПЛТ.
Например, для ранее приведенной задачи 2 ежемесячная выплата клиента составляет:
= ПЛТ (6%/12; 6; -5000) = 847,98 руб.
Размер основного платежа:
= ОСПЛТ (6%/12; 1; 6; -5000) = 822,98 руб.
Размер платежа по процентам:
= ПРПЛТ (6%/12; 1; 6; -5000) = 25,00 руб.
Задача 6.
Организация взяла ссуду в банке в размере 500 тыс. руб. на 10 лет под 10,5% годовых; проценты начисляются ежемесячно.
Определить сумму выплат по процентам за первый месяц и за третий год периода.
Алгоритм решения задачи.
Для вычисления суммы платежей по процентам за требуемые периоды воспользуемся функцией ОБЩПЛАТ (рис. 4.19).
Аргументы функции:Кол_пер = 10*12 = 120 месяцев (общее число выплат); Ставка = 10,5%/12 (процентная ставка за месяц); Нз = 500000 (заем); Тип = 0; для выплаты процентов за 1-й месяц Нач_период = 1 и Кон_период = 1, для выплаты процентов за 3-й год Нач_период = 25 и Кон_период = 36.
Выплата за первый месяц составит:
= ОБЩПЛАТ(10,5%/12; 120; 500; 1; 1; 0) = — 4,375 тыс. руб.
Сумма выплат по процентам за третий год периода составит:
= ОБЩПЛАТ (10,5%/12; 120; 500; 25; 36; 0) = — 44,143 тыс. руб.
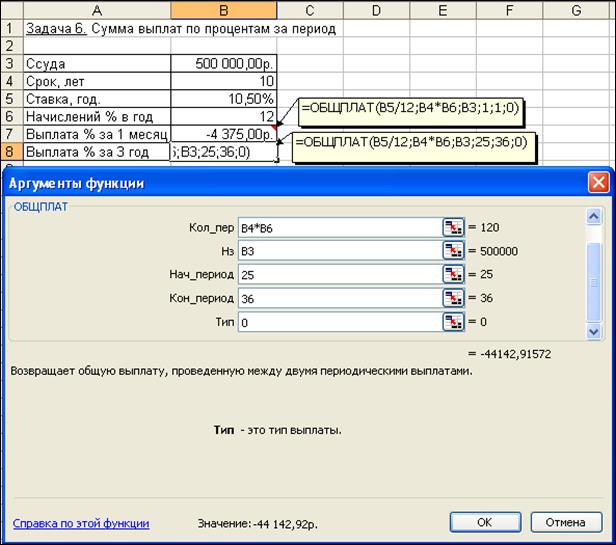
Рис. 4.19. Фрагмент окна с использованием функции ОБЩПЛАТ
Задача 7.
Ссуда размером 1 млн. руб. выдана под 13% годовых сроком на 3 года; проценты начисляются ежеквартально. Определить величину общих выплат по займу за второй год.
Алгоритм решения задачи.
Предположим, что ссуда погашается равными платежами в конце каждого расчетного периода. Тогда для расчета суммы выплаты задолженности за второй год применим функцию ОБЩДОХОД. Аргументы функции: Кол_пер = 3*4 = 12 кварталов (общее число расчетных периодов); Ставка = 13%/4 (процентная ставка за расчетный период – квартал); Нз = 1000000; Нач_период = 5 и Кон_период = 8 (второй год платежа по ссуде – это период с 5 по 8 квартал); Тип = 0.
= ОБЩДОХОД (13%/4; 12; 1000000; 5; 8; 0) = — 331522,23 руб.
Иллюстрация решения задачи представлена на рис. 4.20.
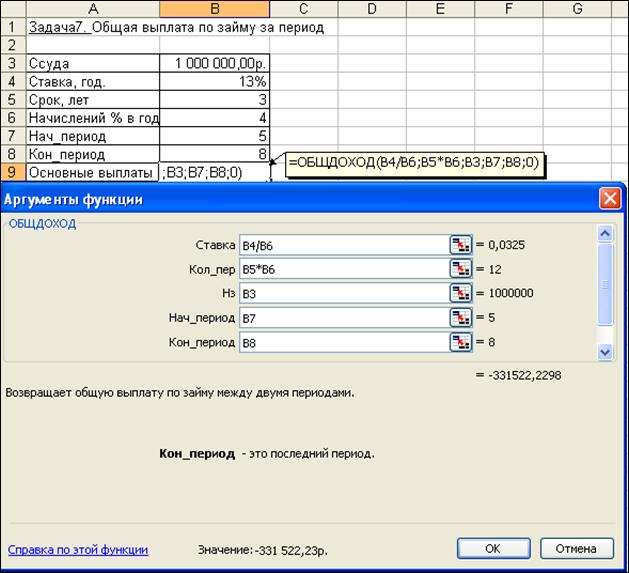
Рис. 4.20. Фрагмент окна с использованием функции ОБЩДОХОД
Задача 8.
Банком выдан кредит в 500 тыс. руб. под 10% годовых сроком на 3 года. Кредит должен быть погашен равными долями, выплачиваемыми в конце каждого года. Разработать план погашения кредита, представив его в виде следующей таблицы:
| Номер периода | Баланс на конец периода | Основной долг | Проценты | Накопленный долг | Накопленный процент |
Алгоритм решения задачи.
Введем исходные данные задачи в ячейки электронной таблицы и определим структуру таблицы плана погашения кредита. Расчет числовых значений выполним с помощью функций Excel. Для получения возможности автозаполнения (копирования) формул, введенных для первого периода плана, на другие периоды, укажем абсолютные ссылки на исходные данные. Иллюстрация решения задачи с указанием примечаний со значениями формул вычислений для 3-го периода приведена на рис. 4.21.

Рис. 4.21. Фрагмент окна с таблицей плана погашения кредита
Приведем также формулы с непосредственным заданием значений аргументов при вычислении плановых данных для 1-го периода:
· размер ежегодного платежа: = ПЛТ (0,1; 3; -500000) = 201 057,40 руб.;
· основной долг: =ОСПЛТ (0,1;1;3;-500000) = 151 057,40 руб.;
· проценты: =ПРПЛТ (0,1; 1; 3; -500000) = ;50 000 руб.;
· накопленный долг: =-ОБЩДОХОД (0,1; 3; 500000; 1; 1; 0) = 151 057,40 руб.;
· накопленный процент: =-ОБЩПЛАТ (0,1; 3; 500000; 1; 1; 0) = 50 000 руб.;
· баланс на конец периода: = Кредит – Накопленный долг = 348 942,60 руб.
Задача 9 .
В целях покупки недвижимости инвестор взял в банке кредит в сумме 12 млн. руб. Определить ежемесячные выплаты по кредиту для разных процентных ставок и сроков погашения кредита.
Алгоритм решения задачи.
Ежемесячные выплаты по займу рассчитываются с использованием функции ПЛТ. Однако аргументы данной функции – процентная ставка и срок погашения кредита – по условию могут принимать различные значения. Поэтому рассмотрим влияние этих параметров на заданную функцию. Воспользуемся механизмом Таблица подстановки из меню команды Данные. Выполним следующую последовательность действий.
1. В ячейку электронного листа С3 введем числовое значение суммы кредита (12 000 000).
2. В ячейки С4, С5 введем произвольные (условные) значения процентной ставки (например, 5%) и срока погашения кредита в годах (например, 1), которые нам понадобятся при построении Таблицы подстановки.
3. В ячейки В9:В22 введем различные значения процентных ставок. В ячейки С9:К9 — возможные сроки погашения.
4. В ячейку В9 введем формулу для расчета ежемесячных выплат по займу: = ПЛТ (5%/12; 1*12; 12 000 000).
Заметим, что в качестве аргументов функции можно вводить как адреса ячеек, так и конкретные исходные значения.
Решение задач из файла «Постановка задач. Пояснения»
Задача 1. Предполагается, что ссуда размером 5000 тыс. рублей погашается ежемесячными платежами по 141,7 тыс. рублей. Рассчитать, через сколько лет произойдет погашение, если годовая ставка процента – 16% (функция КПЕР()). При помощи инструмента Таблица подстановки проанализировать зависимость срока погашения от процентной ставки (10%, 15%, 20%, 25%) и значения платежей (100, 120, 140, 160 и 180 тыс. рублей). Первая часть задачи решается следующим методом:
Рисунок 2. Формула для решения задачи
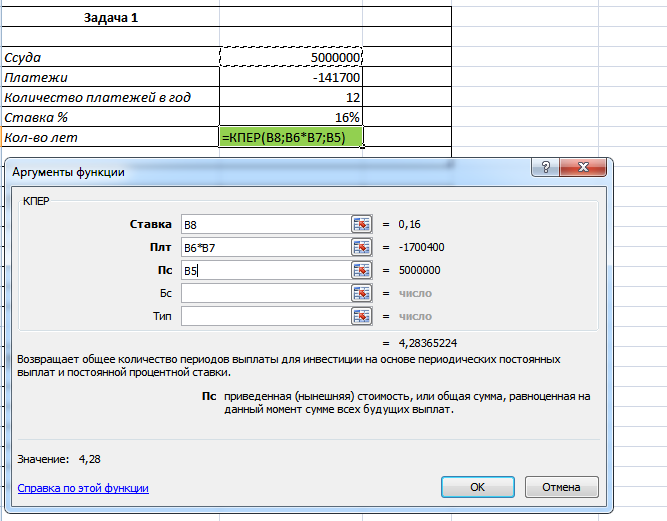
В аргументе «ПЛТ» умножаем ежемесячный платеж на 12, так мы получаем ежегодный платеж, поскольку процентная ставка у нас указана годовая, а не ежемесячная.
Теперь решение второй части задачи (создание таблицы подстановки)
Метод создания таблицы уже был указан выше, поэтому лишь обращу внимание, что адреса на эти аргументы «Подставлять значения по столбцам» и «Подставлять значения по строкам» нужно брать только с условия задачи, иначе таблицу просто не получится создать.
Рисунок 3. Создание таблицы подстановки 1
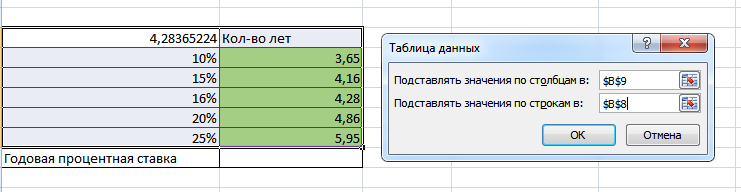
Рисунок 4. Создание таблицы подстановки 2
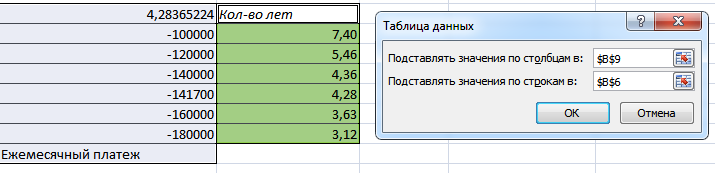
Задача решена, ответ найден, таблицы выведены. Переходим к следующей задаче
Задача 2. Существует два варианта денежных вкладов по 50 тыс. руб. в течение трех лет: в начале каждого года под 19% годовых или в конце каждого года под 27% годовых. Определить наиболее предпочтительный вариант (функция БС(), изменяется аргумент ТИП).
Рисунок 5. Формула для решения задачи

Сначала разбираемся с 1-ым вариантом – где проценты начисляются в начале года. Самое главное в этой функции – значение Тип, здесь мы его ставим на уровень 1, так как проценты начисляются в начале года. Конечная сумма указана ниже на рисунке. Теперь переходим ко 2-му варианту – с начислением процентов в конце года. Процесс такой же, как выше, только лишь с той разницей, что в аргументе Тип мы уже выставляем значение 0 или же оставляем его пустым. В итоге мы видим, что вклад с меньшей процентной ставкой оказался более выгодным, поскольку проценты начислялись в начале каждого года.
Задача 3. Ежегодная плата за приобретенную недвижимость на следующие 25 лет составляет 25 000 рублей. Если считать покупку недвижимости займом с 8% годовых, то какой должна быть его величина, чтобы рассчитаться с займом через 25 лет. (функция ПС())
Рисунок 6. Формула для решения задачи
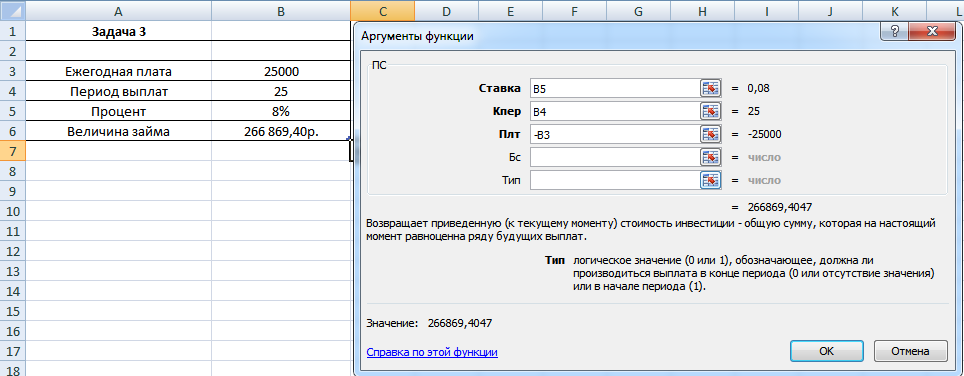
Как видно на рисунке – процесс решения не вызывает сложностей. Открываем функцию ПС, в аргументы проставляем соответствующие значения, и ответ готов.
Задача 4. Рассчитать будущую стоимость облигации номиналом 100 тыс. руб., выпущенной на 4 года, если предусмотрен следующий порядок начисления процентов: в первый год – 12,5%, в следующие два года – 14%, в последний год – 17% годовых БЗРАСПИС (первичное; план).
Рисунок 7. Формула для решения задачи
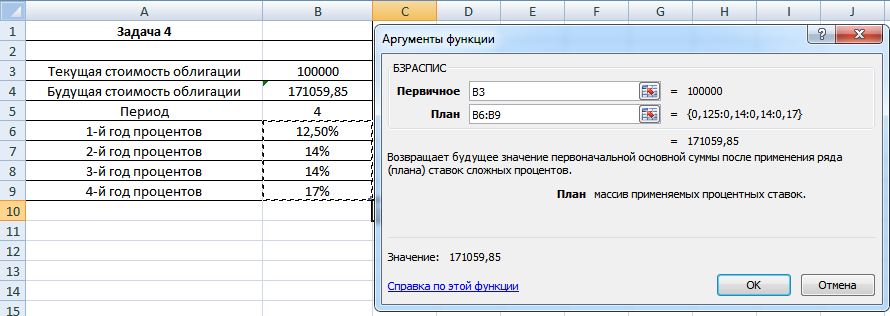
Процесс решения данной задачи также несложен и наглядно виден на изображении.
Задача 5. Ожидается, что будущая стоимость инвестиции размером 150 тыс. руб. к концу четвертого года составит 300 тыс. руб. При этом за первый год доходность составит 15%, за второй – 17%, за четвертый – 23%. Рассчитать доходность инвестиции за третий год, используя аппарат подбора параметра к функции БЗРАСПИС (первичное; план).
Рисунок 8. Формула для решения задачи
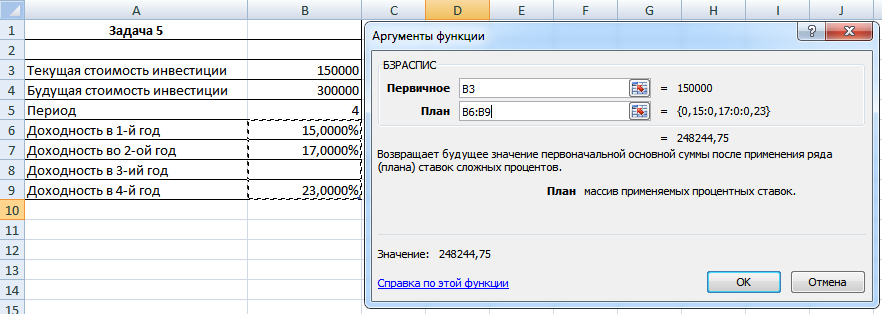
Несмотря на отсутствие значения процентной ставки за 3-ий год – также выделяем все 4 года начисления процентов (пусть 3-ий и отмечен как ноль), делается это в отдельную ячейку. Получится значение, меньшее, чем необходимые нам 300 тысяч, но к указанному значению нам поможет средство под названием Подбор параметра. Находится он там же, где и Таблица подстановки. Мы его запускаем, и видим примерно следующее:
Рисунок 9. Подбор параметра
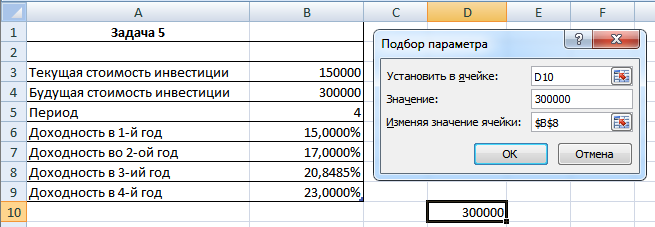
Теперь в этой отдельной ячейке мы должны установить значение в 300 тысяч путем наиболее точного подбора ставки процента на 3-ий год. Здесь указан уже готовый ответ, а поэтому во время подбора нажимаем на пустую ячейку с процентами на 3-ий год, что приведет к подбору точной ставки процента на этот год. Задача решена.
Задача 6. Облигации приобретены 01.07.96 по курсу 79,123 и имеют купонный доход в размере 12%, который выплачивается с периодичностью один раз в год. Предполагаемая дата погашения – 31.12.97 по курсу 100. Определить годовую ставку помещения. Рассчитать аргумент Доход, используя аппарат подбора параметра к функции Цена().
Рисунок 10. Формула для решения задачи
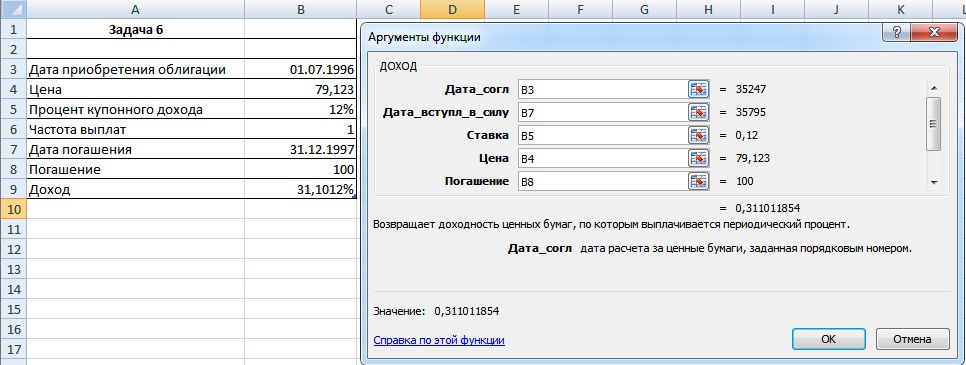
Вышеупомянутый аппарат подбора параметра использовать необязательно, так как и без него можно рассчитать Доход следующим образом: открываем функция Доход, в аргументы ставим соответствующие значения (там ниже в функции указана еще и Частота выплат), и получается ответ, указанный в десятичной дроби (нужно конвертировать в проценты). Задача решена.
Задача 7. Дать заключение по инвестиционному проекту для 5-ти регионов, используя средство Таблица подстановки, если известно, что:
проект рассчитан на 5 лет;
ставка дисконтирования по 1-му региону составляет 5%, по 2-му – 6%, по 3-му – 7%, по 4-му – 8%, по 5-му – 9%.
Финансово-экономические расчеты в Excel
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Методика изучения и использования финансовых функций Excel требует соблюдения определенной технологии.
1. На рабочем листе в отдельных ячейках осуществляется подготовказначений основных аргументов функции.
2. Для расчета результата финансовой функции Excel курсор устанавливается в новую ячейку для ввода формулы, использующей встроенную финансовую функцию; если финансовая функция вызывается в продолжение ввода другой формулы, данный пункт опускается.
3. Осуществляется добавление финансовой функции на рабочий листс помощью команды Формулы, из библиотеки функций активизацией опции Финансовые функции или одновременным нажатием клавиш Shift-F3, а также нажатием одноименной кнопки fx – Вставить функцию на панели инструментов Стандартная.
4. Выполняется выбор категории Финансовые (рис. 2). В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
Рис. 2. Экран вызова опции Вставка функции
В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
5. Выполняется выбор в списке требуемой финансовой функции, в результате выбора появляется диалоговое окно для ввода аргументов (рис. 2). Для каждой финансовой функции существует регламентированный по составу и формату значений перечень аргументов.
6. В поля ввода диалогового окна можно вводить как ссылки на адреса ячеек, содержащих собственно значения аргументов, так и сами значения аргументов.
7. Если аргумент является результатом расчета другой встроеннойфункции Excel, возможно организовать вычисление вложенной встроенной функции путем вызова опции Вставка функции одноименной кнопкой, расположенной перед полем ввода аргумента.
8. Возможна работа с экраном справки, поясняющей назначение иправила задания аргументов функции; вызов справки осуществляется путем нажатия кнопки Справка по этой функции.
9. Для отказа от работы со встроенной функцией нажимается кнопка Отмена.
10. Завершение ввода аргументов и запуск расчета значения встроенной функции выполняется нажатием кнопки ОК.
При необходимости корректировки значений аргументов функции (изменения ссылок, постоянных значений и т.п.) необходимо установить курсор в ячейку, содержащую формулу, и вызвать кнопку fx – Вставить функцию. При этом появляется окно для редактирования (рис. 3).
Рис.3. Диалоговое окно ввода аргументов функции
Возможен вариант непосредственного ввода формулы, содержащей имена и параметры встроенных финансовых функций.
Формула начинается со знака =. Далее следует имя функции, а в круглых скобках указываются её аргументы в последовательности, соответствующей синтаксису функции. В качестве разделителя аргументов используется выбранный при настройке Windows разделитель, обычно это точка с запятой или запятая.
Безусловно, функцию можно ввести, набрав ее прямо в ячейке. Однако Microsoft Excel предоставляет на стандартной панели инструментов кнопку fx – Вставить функцию (см. рис. 4).
Рис. 4. Стандартная панель инструментов (кнопка Вставитьфункцию)
Специфика задания значений аргументов финансовых функций заключается в следующем:
– все аргументы, означающие расходы денежных средств, представляются отрицательными числами (например, ежегодные платежи), а аргументы, означающие поступления, представляются положительными числами (например, дивиденды);
– все даты как аргументы функции имеют числовой формат представления, например, дата 1 января 1995 года представлена числом 34700. Если значение аргумента типа дата берется из ячейки, то дата в ячейке может быть записана в обычном виде;
– для аргументов типа логический возможен непосредственный ввод констант типа ИСТИНА или ЛОЖЬ, либо использование встроенных функций аналогичного названия категории Логические;
– при непосредственном вводе формулы в ячейку необходимо следить за тем, чтобы каждый аргумент находился строго на своем месте. Если какие-то аргументы не используются, то необходимо поставить соответствующее число разделительных знаков. Если не используется последний аргумент или несколько идущих подряд последних аргументов, то соответствующие разделительные знаки можно опустить (в большинстве случаев это замечание относится к аргументам тип и базис).
Для облегчения восприятия материала учебно-методического пособия все финансовые функции и описание их аргументов представлены в прил. 1, табл. 1-6.
В данном разделе показано применение функций Excel, использующих базовые модели финансовых операций. Изложение материала ведется в терминах пакета Excel.
В Excel существует группа функций, предназначенная для расчета финансовых операций по кредитам, ссудам, займам. Эти расчеты основаны на концепции временной стоимости денег, относящихся к разным моментам времени. Эта группа функций охватывает следующие расчеты:
– определение наращенной суммы (будущей стоимости);
– определение начального значения (текущей стоимости);
– определение срока платежа и процентной ставки;
– расчет периодических платежей, связанных с погашением займов.
Понятие будущей стоимости основано на принципе неравноценности денег, относящихся к разным моментам времени. Вложения, сделанные сегодня, в будущем составят большую величину. Эта группа функций позволяет рассчитать:
– будущую или наращенную стоимость серии фиксированных периодических платежей, а также будущую стоимость текущего значения вклада или займа при постоянной процентной ставке;
– будущее значение инвестиции после начисления сложных процентов при переменной процентной ставке.
Во многих задачах используется и понятие текущей (современной) стоимости будущих доходов и расходов. Это понятие базируется на положении о том, что на начальный момент времени полученная в будущем сумма денег имеет меньшую стоимость, чем ее эквивалент, полученный в начальный момент времени.
Согласно концепции временной стоимости денег, расходы и до ходы, не относящиеся к одному моменту времени, можно сопоставить путем приведения к одному сроку (т.е. путем дисконтирования). Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени. Excel содержит ряд функций, которые позволяют рассчитать:
– текущую стоимость единой суммы вклада (займа) и фиксированных периодических платежей;
– чистую текущую стоимость будущих периодических расходов и поступлений переменной величины;
– чистую текущую стоимость нерегулярных расходов и поступлений переменной величины.
Функции для определения срока платежа и процентной ставки позволяют находить величины, расчет которых весьма затруднен, если ведется вручную. К ним относятся:
– общее число периодов постоянных выплат, необходимых для достижения заданного будущего значения; число периодов, через которое начальная сумма займа (вклада) достигнет заданного значения;
– значение постоянной процентной ставки за один период серии фиксированных периодических платежей; значение ставки процента по вкладу или займу.
При выпуске ценных бумаг, заключении финансовых контрактов, займах на долговом соглашении указывается годовая номинальная процентная ставка и период начисления (год, полугодие, квартал).
Начисление процентов по номинальной ставке производится по формуле сложных процентов. Годовая ставка, обеспечивающая тот же доход, что и номинальная ставка после начисления сложных процентов, – это эффективная процентная ставка. Номинальная и эффективная процентная ставки эквивалентны по финансовому результату.
Функции Excel также позволяют вычислять следующие величины, связанные с периодическими выплатами:
– периодические платежи, осуществляемые на основе постоянной процентной ставки и не меняющиеся за все время расчета;
– платежи по процентам за конкретный период;
– сумму платежей по процентам за несколько периодов, идущих основные платежи по займу (за вычетом процентов) за конкретный период;
– сумму основных платежей за несколько периодов, идущих подряд.
Все эти величины вычисляются, например, при расчете схемы равномерного погашения займа. Допустим, что заем погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость этих платежей будет равна сумме займа с начисленными процентами к концу последнего расчетного периода, если в нем предполагается полное погашение займа.
С другой стороны, текущая стоимость выплат по займу должна равняться настоящей сумме займа. Если известна сумма займа, ставка процента, срок, на который выдан заем, то можно рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа.
: Предположим, что открыт льготный (не облагаемый налогами) пенсионный счет. При этом планируется вносить на счет 2000$ в начале каждого года в расчете на среднюю скорость оборота 11 % в год на протяжении всего срока. Если считать, что клиенту сейчас 30 лет, то какая сумма будет аккумулирована на его счету, когда ему исполниться 65 лет, и если клиент открыл счет три года назад и на настоящий момент уже накопил 7500$?
Рис. 5. Пример решения задачи по теме: «Функции для расчета операций по кредитам и займам»
1. Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положенына 33 года под 13,5 % годовых. Проценты начисляются каждые полгода.
2. Предположим, есть два варианта инвестирования средств в течение 4лет: в начале каждого года под 26 % годовых или в конце каждого года под 38 % годовых. Пусть ежегодно вносится 300 тыс. руб. Определить, сколько денег окажется на счете в конце 4-го года для каждого варианта.
3. Предположим, Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6 % годовых (что составит в месяц 6 %/12 или 0,5 %). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?
4. Рассчитать, какая сумма будет на счете, если сумма размером5000 тыс. руб. размещена под 12 % годовых на 3 года, а проценты начисляются каждые полгода.
5. По вкладу размером 2000 тыс. руб. начисляется 10 % годовых.Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.
6. На сберегательный счет вносятся платежи по 200 тыс. руб. в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 % годовых.
7. На сберегательный счет вносятся платежи по 200 тыс. руб. в конце каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 % годовых.
8. По облигации номиналом 100 тыс. руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10 %, в два последующих года – 20 %, в оставшиеся три года – 25 %. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
9. Исходя из плана начисления процентов, приведенного в предыдущей задаче, рассчитать номинал облигации, если известно, что ее будущая стоимость составила 1546,88 тыс. руб. При решении использовать аппарат подбора параметра программы Excel.
10. Рассчитать будущую стоимость облигации номиналом 300 тыс. руб., выпущенной на 5 лет, если предусмотрен следующий порядок начисления процентов: в первые два года – 13,5 % годовых, в следующие два года – 15 % и в последний год – 20 % годовых.
11. Ожидается, что будущая стоимость инвестиции размером 1500 тыс. руб. к концу 4-го года составит 3000 тыс. руб. При этом за первый год доходность составит 15 %, за второй – 17 %, за четвертый – 23 %. Рассчитать доходность инвестиции за третий год. При решении использовать аппарат Подбора параметра Excel.
12. Предположим, что представилась возможность вложения, которое ежегодно возвращает 1000$ в течение следующих пяти лет. Но для этого нужно вложить 4000$. Имеет ли смысл выкладывать 4000$ сегодня, чтобы заработать 5000$ в течение следующих пяти лет? Для решения задачи определить текущую стоимость ряда поступления, полагая, что деньги можно положить на краткосрочный счет под 4,5 % (барьерная ставка).
13. Используя данные из предыдущего примера, предположим, что клиент получит 5000$ в конце пятого года, а не по 1000$ в каждый из последующих пяти годов. Будет ли это вложение выгодным?
14. Имеется возможность вложения капитала, которое обещает принести убыток в размере 55000$ в конце первого года, но затем дать прибыль 95000$, 140000$ и 185000$ в конце второго, третьего и четвертого года. При этом необходимо вложить авансом 250000$, а барьерная ставка должна быть равна 12 %. Можно ли рассчитывать на получение чистой прибыли от этого вложения?
15. Предположим, что Вы намерены выкупить страховку, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 % годовых. Вы хотите определить, будет ли это хорошим способом инвестировать капитал. Какую финансовую функцию необходимо использовать, чтобы рассчитать настоящий объем вклада?
16. Фирме потребуется 5000 тыс. руб. через 12 лет. В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы через 12 лет он достиг 5000 тыс. руб. Определить необходимую сумму текущего вклада, если ставка процента по нему составляет 12 % в год.
17. Предположим, рассматриваются два варианта покупки дома: заплатить сразу 99000 тыс. руб. или в рассрочку – по 940 тыс. руб. ежемесячно в течение 15 лет. Определить, какой вариант предпочтительнее, если ставка процента – 8 % годовых.
18. Рассчитать текущую стоимость вклада, который через три года составить 15000 тыс. руб. при начислении 20 % в год.
19. Определить текущую стоимость обязательных ежемесячных платежей размером 100 тыс. руб. в течение 5 лет, если процентная ставка составляет 12 % годовых.
20. Определить текущую стоимость обычных ежемесячных платежейразмером 50 тыс. руб. в течение двух лет при начислении 18 % годовых.
21. Рассчитайте, какую сумму необходимо положить на депозит, чтобы через 4 года она достигла значение 20 млн. руб. при начислении 9 % годовых.
22. Определить текущую стоимость обычных ежеквартальных платежей размером 350 тыс. руб. в течение 7 лет, если ставка процента 11 % годовых.
23. Рассмотрим инвестицию, при которой Вы выплачиваете 10000 руб. через год после сегодняшнего дня и получаете годовые доходы 3000 руб., 4200 руб. 6800 руб. в последующие три года. Предположим, что учетная ставка составляет 10 %, в таком случае рассчитайте чистый текущий объем инвестиции.
24. Рассмотрим инвестиции, которые начинаются в начале первого периода. Допустим, Вы интересуетесь покупкой обувного магазина. Стоимость предприятия – 40 000 руб. и Вы ожидаете получить следующие доходы за первые пять лет: 8 000 руб., 9 200 руб., 10 000 руб., 12 000 руб. и 14 500 руб. Годовая учетная ставка равна 8 %. Она может представлять степень инфляции или учетную ставку конкурирующих инвестиций. Если стоимость и доходы от обувного магазина введены в ячейки от B1 до B6 соответственно, то чему будет равен чистый текущий объем инвестиции в обувной магазин?
25. На основании данных из предыдущей задачи (24) предположим, что на шестой год Ваш магазин потерпел крах, и Вы предполагаете убыток в 9000 руб. для шестого года. Чему будет равен чистый текущий объем инвестиции в обувной магазин после шести лет?
26. Инвестиции в проект к концу первого года его реализации составят 10000 руб. В последующие три года ожидаются годовые доходы по проекту 3000 руб., 4200 руб.. 6800 руб. Издержки привлечения капитала 10 %. Рассчитать чистую текущую стоимость проекта.
27. Можно приобрести оборудование за 40000 руб. наличными. Можно вложить наличность под 8 %. В течение пяти последующих лет в конце каждого года оборудование экономит: 9000, 6000, 6000, 5000 и 5000 руб. соответственно. В конце шестого года оборудование экономит 5000 руб., и его можно продать за 25000 руб. Стоит ли делать такую покупку?
28. Допустим затраты по проекту в начальный момент его реализации составляют 37000 руб., а ожидаемые доходы за первые пять лет: 8000 руб., 9200 руб., 10000 руб., 13900 руб. и 14500 руб. На шестой год ожидается убыток в 5000 руб. Цена капитала 8 % годовых. Рассчитать чистую текущую стоимость проекта.
29. Определить эффективность инвестиций размером 200 млн. руб.по NPV, если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 20, 40, 50, 80 и 100 млн. руб. Издержки привлечения капитала составляют 13,5 % годовых.
30. Рассчитать чистую текущую стоимость проекта, затраты по которому составят 400 млн. руб., а предполагаемые доходы за первые два года реали зации проекта – 40 и 80 млн. руб. Начало реализации проекта – через два года. Норма дисконтирования – 15 % годовых.
31. Инвестиция размером 10 млн. руб. от 01.07.1998 года, которая принесет доходы: 2750 тыс. руб. на 15.09.1998 года, 4250 тыс. руб. на 01.11.1998 года, 5250 тыс. руб. на 01.01.1999 года. Норма дисконтирования 9 %. Определить чистую текущую стоимость инвестиции на 01.07.1998 года и на 01.07.1997 года.
32. Определить чистую текущую стоимость проекта на 1.01.1998, затраты по которому на 20.12.1998 составят 100 млн. руб. Ожидается, что за первые полгода 1999 года проект принесет следующие доходы: на 01.03.1999 –18 млн. руб.; на 15.04.1999 – 40 млн. руб.; на 30.06.1999 – 51 млн. руб. Норма дисконтирования – 12 % годовых.
33. Рассмотрим инвестицию, при которой предполагается выплата наличными 10000 руб. 01.01.1992 года и поступления: 2750 руб. 01.03.1992 года, 4250 руб. 30.10.1992 года, 3250 руб. 15.02.1993 года и 2750 руб. 01.04.1993 года. Определить чистую текущую стоимость инвестиций.
34. Рассчитать, через сколько лет вклад размером 1 млн. руб. достигнет величины 1 млрд. руб., если годовая ставка процента по вкладу 16,79 % и начисление процентов производится ежеквартально.
35. Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Размер разового платежа 16 млн. руб. На поступившие взносы начисляется 11,18 % годовых. Необходимо определить, когда величина фонда будет равна 100 млн. руб.
36. Ожидается, что ежегодные доходы от реализации проекта составят 33 млн. руб. Необходимо рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн. руб., а норма дисконтирования 12,11 %.
37. Ссуда размером 66000 тыс. руб., выданная под 36 % годовых, погашается обычными ежемесячными платежами по 6630 тыс. руб. Определить срок погашения ссуды.
38. Клиент может выплачивать по закладной 1000$ в месяц. Каков срок, в течение которого он выплатит 100000$, взятых под 8 % годовых.
39. Определить общее количество периодов выплаты для вклада 10000 руб. на основе периодических постоянных выплат, составляющих 100 руб., при общей сумме всех будущих платежей в 1000 руб. и постоянной процентной ставке 12 % годовых.
40. Через сколько лет обязательные ежемесячные платежи размером 150 тыс. руб. принесут доход в 10 млн. руб. при ставке процента 13,5 % годовых?
41. Рассчитать, через сколько лет произойдет полное погашение займа размером 500 тыс. руб., если выплаты по 100 тыс. руб. производятся в конце каждого квартала, а ставка процента – 15 % годовых.
Источник https://studopedia.ru/18_6813_argumenti-finansovih-funktsiy-Excel-analiza-investitsiy.html
Источник https://studfile.net/preview/4078911/page:2/
Источник https://www.livelib.ru/book/141688/readpart-finansovoekonomicheskie-raschety-v-excel-evgenij-shirshov/~4